Categoría: Matemáticas

Operaciones entre conjuntos

Anthonny Arias-García2 comentarios
  1. Unión de Conjuntos
    1. Ejemplos
      1. Ejemplo 1
      2. Ejemplo 2
      3. Ejemplo 3
  2. Intersección de Conjuntos
    1. Ejemplos
      1. Ejemplo 4
      2. Ejemplo 5
      3. Ejemplo 6
  3. Complemento de un Conjunto
    1. Ejemplos
      1. Ejemplo 7
      2. Ejemplo 8
      3. Ejemplo 9
  4. Diferencia de Conjuntos
    1. Ejemplos
      1. Ejemplo 1
      2. Ejemplo 2
      3. Ejemplo 3

Al considerar dos conjuntos A y B, son diversas las operaciones que se pueden definir sobre ellos dos. Sin embargo, todas se basan en las operaciones de unión, intersección y el complemento. A continuación estudiaremos de forma concisa cada una de estas operaciones apoyándonos en Diagramas de Venn y usando conjuntos numéricos.

También pudiera interesarte

Unión de Conjuntos

Dados dos conjuntos A y B, definiremos la unión de estos dos conjuntos como un nuevo conjunto que contiene todos los elementos de A junto con todos los elementos de B y la denotaremos por A \cup B. Si consideramos un elemento c del conjunto A \cup B entonces c pertenece a A o pertenece a B.

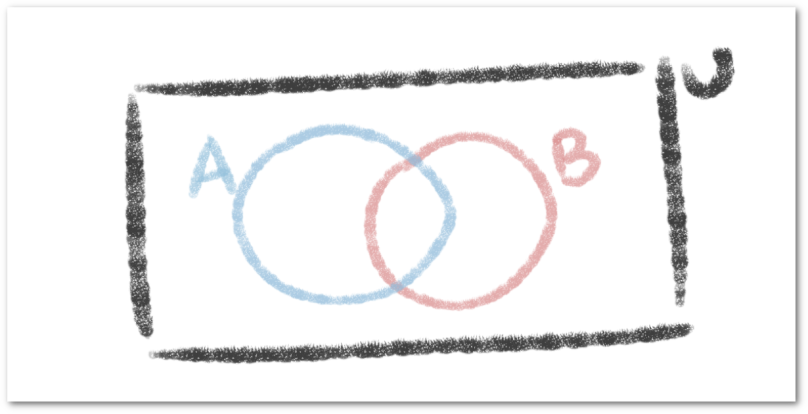
Los Diagramas de Venn nos ayudan a expresar visualmente los conjuntos para entender algunas ideas, usualmente se usan círculos para representar conjuntos contenidos en un universo rectangular. A continuación, usaremos un Diagrama de Venn para expresar visualmente la unión entre dos conjuntos.

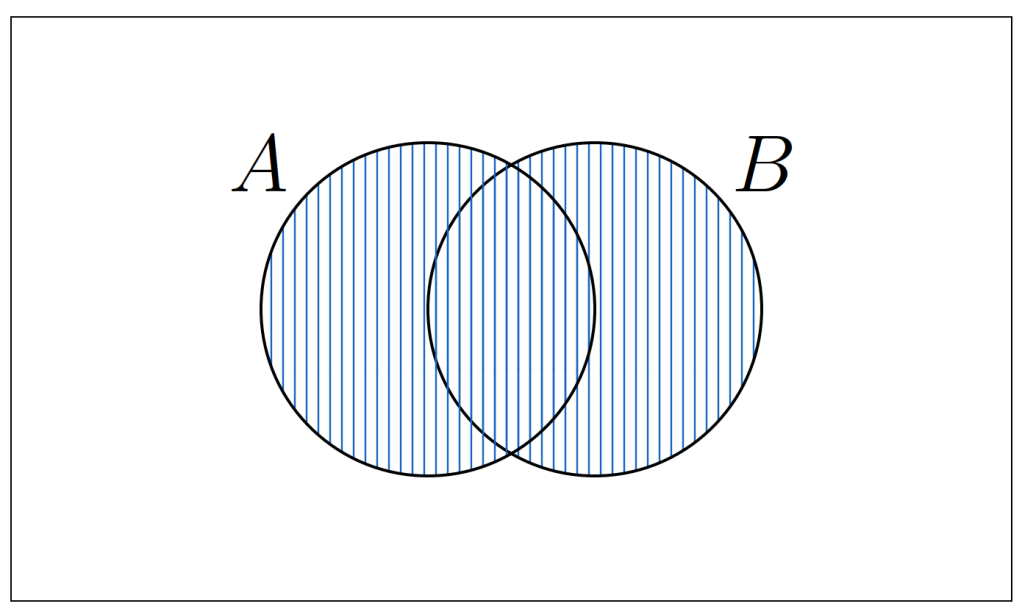
Ejemplos

Ejemplo 1

Dentro de la Facultad de Ciencias Económicas y Sociales, la unión del conjunto de todos los estudiantes que miden menos de un metro con cincuenta centímetros con el conjunto de todos los estudiantes que miden más o incluso un metro con cincuenta centímetros es el conjunto de todos los estudiantes de la Facultad de Ciencias Económicas y Sociales.

Ejemplo 2

La unión del conjunto \{1,2,3,4\} con el conjunto \{5,6,7\} es el conjunto \{1,2,3,4,5,6,7\}, es decir,

\{1,2,3,4\} \cup \{5,6,7\} = \{1,2,3,4,5,6,7\}

Ejemplo 3

La unión del conjunto \{3,4,5,6,7,8\} con el conjunto \{5,6,7,8,9,10,11\} es el conjunto \{3,4,5,6,7,8,9,10,11\}, es decir,

\{3,4,5,6,7,8\} \cup \{5,6,7,8,9,10,11\} = \{3,4,5,6,7,8,9,10,11\}

Notemos que aunque hay elementos comunes en ambos conjuntos, estos sólo se cuentan una vez en la unión de los dos conjuntos.

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.

Intersección de Conjuntos

Por otra parte si consideramos nuevamente dos conjuntos A y B, definiremos la intersección entre estos dos conjuntos como un nuevo conjunto que contiene todos los elementos que están en A y que están en B al mismo tiempo, y lo denotaremos por A \cap B . Si consideramos un elemento c de A \cap B entonces c pertenece a A y pertenece a B al mismo tiempo. En el siguiente Diagrama de Venn, la intersección de los conjuntos queda representada por el área donde las líneas se cruzan.

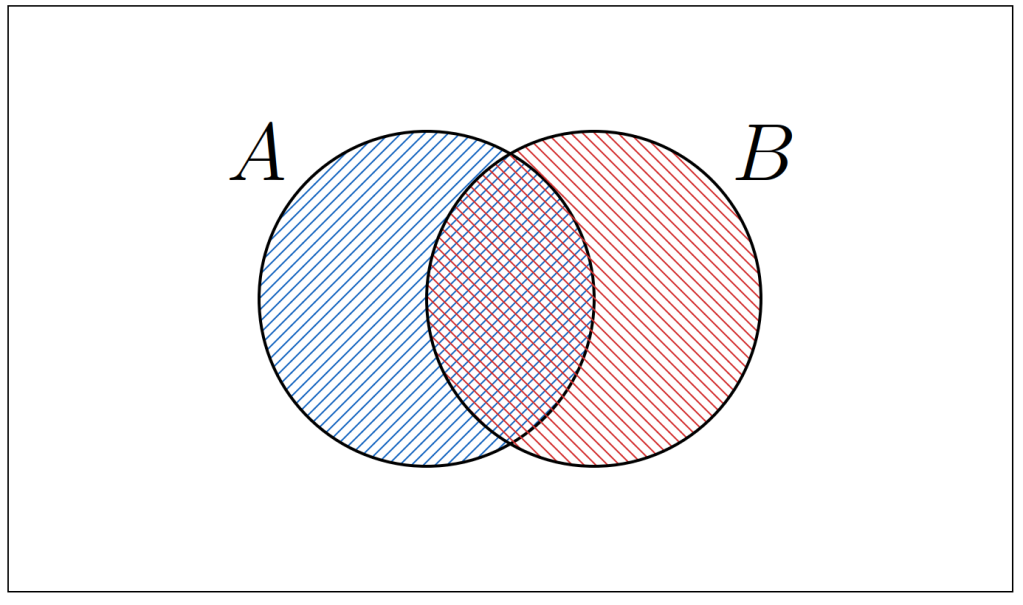
Ejemplos

Ejemplo 4

Dentro de la Facultad de Ciencias Económicas y Sociales, la intersección del conjunto de todos los estudiantes de sexo masculino con el conjunto de todos los estudiantes que tienen un promedio de calificaciones de 10 puntos es el conjunto de todos los estudiantes de sexo masculino con un promedio de calificaciones de 10 puntos en la Facultad de Ciencias Económicas y Sociales.

Ejemplo 5

La intersección del conjunto \{1,2,3,4,5,6\} con el conjunto \{5,6,7,8,9,10,11\} es el conjunto \{5,6\}, es decir,

\{1,2,3,4,5,6\} \cap \{5,6,7,8,9,10,11\} = \{5,6\}

Ejemplo 6

La intersección del conjunto \{1,2,3,4\} con el conjunto \{5,6,7\} es un conjunto que no tiene elementos y que llamaremos el conjunto vacío, lo denotaremos de la siguiente forma

\{1,2,3,4\} \cup \{5,6,7\} = \varnothing

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.

Complemento de un Conjunto

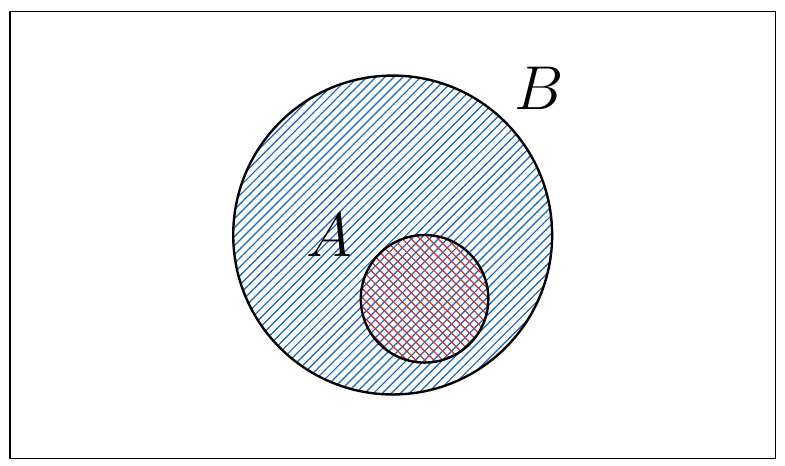
Diremos que el Universo (conjunto universal) es el contexto donde están definidos nuestros conjuntos, en él estarán contenidos todos los conjuntos de nuestro estudio. Por ejemplo, podemos considerar un conjunto A igual a \{2,4,6\} en el universo \{1,2,3,4,5,6,7,8,9,10\}.

Sentando base en esto, si consideramos un conjunto A, definiremos el Complemento de A como un conjunto especial que está definido como todos los elementos que no están en A y lo denotaremos por A^{c}. Si consideramos un elemento c de A^{c} entonces c no está en A. En el siguiente Diagrama de Venn, representaremos este conjunto

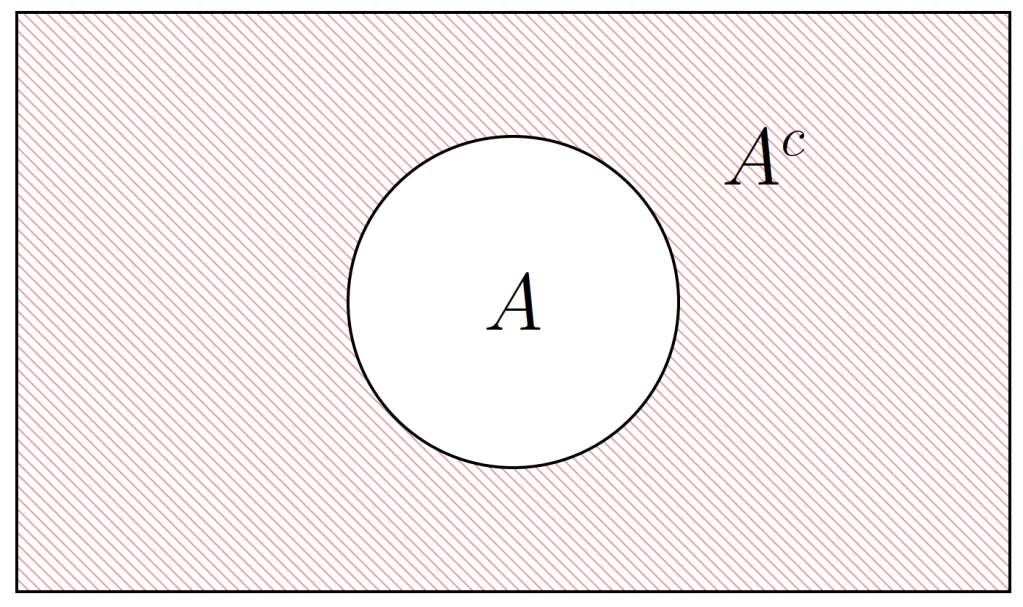
Ejemplos

Ejemplo 7

Dentro de la Facultad de Ciencias Económicas y Sociales, el complemento del conjunto de las personas que miden más o incluso un metro con ochenta centímetros es el conjunto de las personas que miden menos de un metro con ochenta centímetros.

Ejemplo 8

En el universo \{1,2,3,4,5,6,7,8,9,10,11\}, el complemento del conjunto \{1,2,3,4,5,6\} es el conjunto \{7,8,9,10,11\}, es decir,

\{1,2,3,4,5,6\}^{c} = \{7,8,9,10,11\}

Ejemplo 9

En el universo \{5,6,7,8,9\}, el complemento del conjunto \{5,6,7,8,9\} es un conjunto que no tiene elementos y que llamaremos el conjunto vacío, lo denotaremos de la siguiente forma, es decir,

\{5,6,7,8,9\}^{c} = \varnothing

Nota: De forma general, diremos que U^{c} = \varnothing y que \varnothing^{c} = U.

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.

Diferencia de Conjuntos

Considerando las operaciones entre conjuntos, pudiéramos asociar la unión de conjuntos como una suma, entonces, ¿se podrá definir una operación parecida a la resta? Dados dos conjuntos A y B, definiremos la diferencia del conjunto A menos el conjunto B como un nuevo conjunto que contiene todos los elementos que están en A y que no están en B; y la denotaremos por A / B latex ó A - B. Si consideramos un elemento c de A / B latex entonces $c$ pertenece a A y no pertenece a B. En el siguiente Diagrama de Venn, representaremos este conjunto

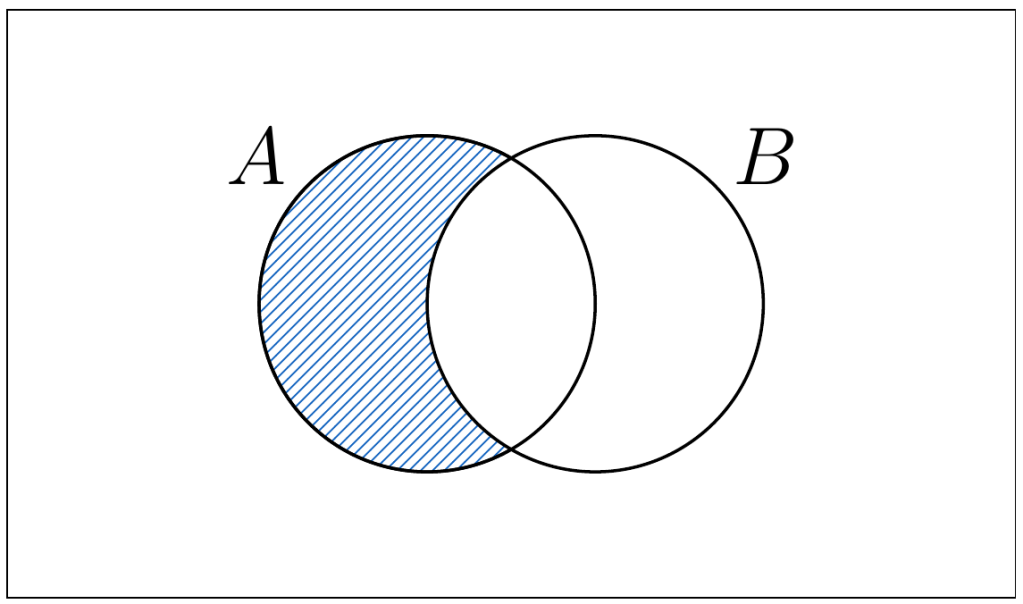
Ejemplos

Ejemplo 1

Dentro de la Facultad de Ciencias Económicas y Sociales, la diferencia de todos los estudiantes que tienen un promedio de calificaciones de 10 menos todas las estudiantes de sexo femenino es igual a todos los estudiantes de sexo masculino que tienen un promedio de calificaciones de 10.

Ejemplo 2

La diferencia del conjunto {1,2,3,4,5,6} menos el conjunto \{4,5,6,7,8,9,10,11\} es el conjunto \{1,2,3\}, es decir,

\{1,2,3,4,5,6\} / \{5,6,7,8,9,10,11\} = \{1,2,3\}

Ejemplo 3

La diferencia del conjunto \{1,2,3,4\} menos el conjunto \{8,9,10\} es el conjunto \{1,2,3,4\}, es decir,

\{1,2,3,4\} / \{8,9,10\} = \{1,2,3\}

Conjuntos

Anthonny Arias-GarcíaDeja un comentario
  1. ¿Qué es un conjunto?
  2. Notación matemática de un conjunto
  3. Subconjuntos
    1. Ejemplos
      1. Ejemplo 1
      2. Ejemplo 2
      3. Ejemplo 3

¿Qué es un conjunto?

Un Conjunto es una agrupación de objetos de cualquier índole. Por ejemplo: El conjunto de los días de la semana, el conjunto de los meses de un año, el conjunto de los colores del arcoiris, el conjunto de los números que puedo contar con los dedos de una mano, el conjunto de carros en concesionario, el conjunto de los alumnos inscritos en una institución, el conjunto de gatos en una casa o el conjunto de granos de arena en una playa.

También pudiera interesarte

Generalmente consideraremos conjuntos cuyos objetos posean una característica en común. Por ejemplo,

  • Lunes, Martes, Miércoles, Jueves, Viernes Sábado, Domingo
  • rojo, naranja, amarillo, verde, azul, indigo, violeta
  • 1,2,3,4,5
  • Alumnos inscritos en la Facultad de Ciencias Económicas y Sociales
  • Carros en un concesionario, tales que sean azules

Note que en el último ejemplo, primero definimos el objeto (los carros) y después describimos la característica común que tienen todos los elementos del conjunto (que sean azules).

Notación matemática de un conjunto

Podemos describir a los conjuntos de dos formas:

  • Extensivamente: nombrando todos los elementos del conjunto.
  • Comprensivamente: indicando cuales son los elementos y al menos una propiedad común que tengan todos los elementos del conjunto.

La notación que usaremos para escribir los conjuntos será encerrando sus elementos o describiendo su propiedad común entre llaves entre llaves \{ \ \ \ \}. Por ejemplo,

Podemos definir el conjunto de todos los números pares extensivamente de la siguiente forma:

\displaystyle \{ 2,4,6,8,10, 12, \ldots\}

Por otra parte, también podemos definir este mismo conjunto comprensivamente de la siguiente forma:

\displaystyle \{ 2n : n \in \mathbb{N} \}

Los dos puntos : se leen tal que y así, este último conjunto se lee El conjunto de los números de la forma 2 \cdot n tales que n es un número natural.

Usualmente denotaremos los conjuntos con letras mayúsculas tales como A, B, C, D, \ldots; a cada objeto perteneciente al conjunto lo llamaremos elemento del conjunto y los denotaremos con letras minúsculas tales como a, b, c, d, \ldots. Para denotar que un elemento a está en un conjunto A escribimos,

\displaystyle a \in A

Esto se lee a pertenece al conjunto A.

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.

Subconjuntos

Un subconjunto de un conjunto es una agrupación de elementos que pertenece a un conjunto de elementos. Por ejemplo:

  • El conjunto de carros azules en un concesionario, es un subconjunto del conjunto de carros en un concesionario.
  • El conjunto de los alumnos menores de edad inscritos en una universidad, es un subconjunto del conjunto de alumnos en una universidad.
  • El conjunto de gatos negros en un albergue de mascotas, es un subconjunto del conjunto de gatos en un albergue de mascotas.

Para denotar que un conjunto A es subconjunto de un conjunto B, escribimos

\displaystyle A \subset B

Esto se lee «A está contenido en B» y en el siguiente Diagrama de Venn representamos un conjunto contenido dentro de otro.

Un círculo pequeño A rayado con rojo, dentro de un círculo más grande B rayado con azul. | totumat.com

Ejemplos

Ejemplo 1

El conjunto formado por los días sábado y domingo, es un subconjunto del conjunto de los días de la semana, es decir,

{Sábado, Domingo} \subset {Lunes, Martes, Miércoles, Jueves, Viernes, Sábado, Domingo}

Ejemplo 2

El conjunto de los números \{1,2,3,4\} es un subconjunto del conjunto \{1,2,3,4,5,6,7,8,9,10\}, es decir,

\{1,2,3,4\} \subset \{1,2,3,4,5,6,7,8,9,10\}

Ejemplo 3

El conjunto de los alumnos de alto promedio Inscritos en la Facultad de Ciencias Económicas y Sociales es un subconjunto de los Alumnos inscritos en la Facultad de Ciencias Económicas y Sociales.