Hemos calculado anteriormente la integral de la función usando el método de sustitución de variable, pero si consideramos una función levemente distinta ¿podemos usar usar nuevamente el método de sustitución de variable?
También pudiera interesarte
Supongamos que queremos calcular la integral de la función . Por más que pensemos en una variable auxiliar que nos pueda ayudar a calcular esta integral, no la encontraremos. Entonces, debemos desarrollar un método que nos permita calcular la integral de este tipo de funciones.
Si y
son dos funciones, entonces a partir de la Regla del Producto para la derivada de funciones, podemos concluir lo siguiente
El Método de Integración por Partes
A esta igualdad la llamaremos El Método de Integración por Partes y aunque pareciera un poco intrincada, existe una regla mnemotécnica, es decir, un juego de palabras muy divertido para aprendérsela de memoria con facilidad recurriendo a dos variables auxiliares y
planteando lo siguiente
un día vi una vaca sin cola vestida de uniforme
Una vez identificados los factores y
que están involucrados en la integral notamos que además de estas dos variables debemos contar también con
y
para poder aplicar el método de integración por partes. ¿Cómo lo hacemos?
- Calculamos
a partir de
usando las técnicas de derivación que conocemos.
- Calculamos
a partir de
usando las técnicas de integración que conocemos.
Veamos entonces como aplicar este método para calcular la integral de la función , es decir,
Para este caso en particular podemos considerar y
, entonces
Notemos que hemos descartado la constante al calcular
. Al estar definidos cada uno de los elementos del método de integración por partes, tenemos que

Sólo resta calcular la integral que está en el lado derecho de la igualdad, es decir,
Una vez que hemos calculado esta integral, sustituimos su resultado donde corresponde para obtener que
La idea de este método es obtener del lado derecho de la igualdad una integral más simple de la que estamos calculando originalmente. Veamos en lo siguientes ejemplos las estrategias para proceder usando este método.
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ejemplos
Ejemplo 1
Calcule la integral de , es decir,
Al aplicar el método de integración por partes, la escogencia de los factores y
es de vital importancia para calcular la integral propuesta, es por esto que no nos debemos confiar en el orden que estos aparecen a primera vista. Cambiemos entonces el orden de los factores para plantear lo siguiente

Al estar definidos cada uno de los elementos del método de integración por partes, tenemos que

Sólo resta calcular la integral que está en el lado derecho de la igualdad, es decir,
Una vez que hemos calculado esta integral, sustituimos su resultado donde corresponde para obtener que
Nota: Se invita a lector a verificar si el calculo de la integral es más simple o más complicado con otra escogencia de factores.
Ejemplo 2
Calcule la integral de , es decir,
Al aplicar el método de integración por partes, la escogencia de los factores y
es de vital importancia para calcular la integral propuesta, escojamos en este caso

Al estar definidos cada uno de los elementos del método de integración por partes, tenemos que

Sólo resta calcular la integral que está en el lado derecho de la igualdad, es decir,
Una vez que hemos calculado esta integral, sustituimos su resultado donde corresponde para obtener que
Nota: Se invita a lector a verificar si el calculo de la integral es más simple o más complicado con otra escogencia de factores.
Ejemplo 3
Calcule la integral de , es decir,
Al aplicar el método de integración por partes, la escogencia de los factores y
es de vital importancia para calcular la integral propuesta, escojamos en este caso

Al estar definidos cada uno de los elementos del método de integración por partes, tenemos que

Sólo resta calcular la integral que está en el lado derecho de la igualdad, es decir,
Una vez que hemos calculado esta integral, sustituimos su resultado donde corresponde para obtener que
Nota: Se invita a lector a verificar si el calculo de la integral es más simple o más complicado con otra escogencia de factores.
En estos ejemplos hemos visto los casos más básicos del Método de Integración por Partes para facilitar su entendimiento, sin embargo, hay casos para funciones más complejas en las que se puede usar.
Algunos memes del Método de Integración por Partes










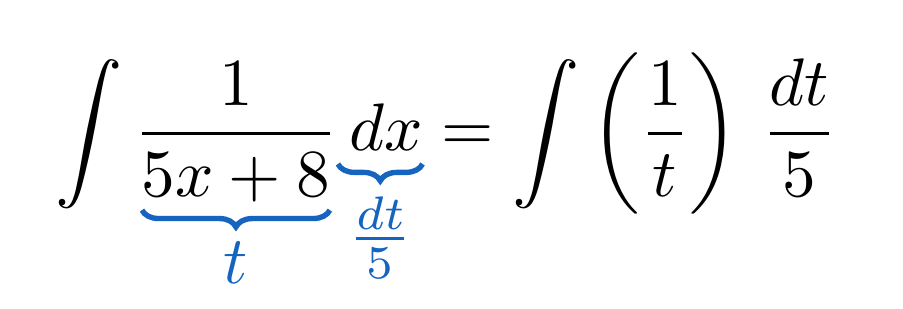



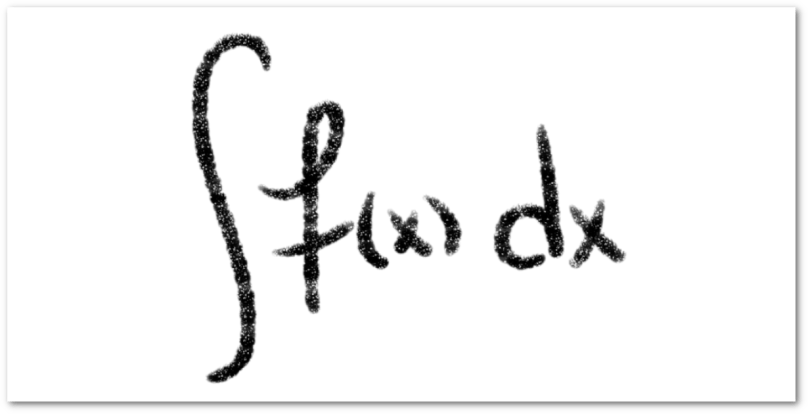
Debe estar conectado para enviar un comentario.