Expresiones Logarítmicas
En ocasiones, encontramos ecuaciones exponenciales cuya solución no es una tarea trivial, así que debemos recurrir a métodos más sofisticados. Si  y
y  son números reales positivos, definimos una nueva expresión a partir de la siguiente equivalencia:
son números reales positivos, definimos una nueva expresión a partir de la siguiente equivalencia:

La expresión  se conoce como una expresión logarítmica y se lee como logaritmo base a de b. Esta provee una solución para la ecuación planteada.
se conoce como una expresión logarítmica y se lee como logaritmo base a de b. Esta provee una solución para la ecuación planteada.
De forma particular, si consideramos la ecuación exponencial  , entonces, podemos usar una expresión logarítmica para definirla de la siguiente manera
, entonces, podemos usar una expresión logarítmica para definirla de la siguiente manera
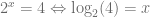
La importancia de las expresiones logarítmicas radica en que estas se usan principalmente para describir variaciones proporcionales, porcentuales o en el largo plazo sobre conjuntos de datos, es por esto que son ampliamente estudiadas. Veamos entonces cuales son sus propiedades.
Propiedades del Logaritmo
Propiedades sobre el argumento
A continuación se presentará una lista de algunas propiedades del logaritmo de un número, del producto y la división, que se deducen de las propiedades de la potencias. Sean  y
y  números reales positivos;
números reales positivos; 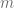 y
y  números reales, entonces
números reales, entonces
Propiedades sobre la base
Las propiedades antes vistas, hacen referencia al argumento del logaritmo, es decir, a la expresión que se encuentra dentro de los paréntesis. Sin embargo, la propiedad que veremos a continuación hace referencia a la base de estos y se conocen como propiedades de cambio de base.
Si consideramos el logaritmo base  de b,
de b,  y consideramos un nuevo número real positivo
y consideramos un nuevo número real positivo  . Entonces, este logaritmo se puede reescribir de la siguiente manera
. Entonces, este logaritmo se puede reescribir de la siguiente manera

De esta forma, hemos reescrito el logaritmo que originalmente tenía base  como el cociente de dos logaritmos de base
como el cociente de dos logaritmos de base  .
.
Ecuaciones Logarítmicas
Si bien se pueden presentar casos en los que una incógnita se presenta en el argumento o en la base logaritmo en una ecuación, también hay que considerar los logaritmos serán de vital importancia al calcular la solución de ecuaciones exponenciales donde la base de los elementos involucrados no es la misma.
Veamos algunos ejemplos en los que empleamos las propiedades de los logaritmos para calcular la solución de ecuaciones que involucran expresiones logarítmicas.
Ejemplos
Ejemplo 1
Calcule la solución de la siguiente ecuación logarítmica:
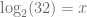
Si bien podemos calcular 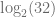 directamente con una calculadora, este tipo de ecuaciones sirve como ejercicio para familiarizase con las propiedades de las potencias y las propiedades de los logaritmos.
directamente con una calculadora, este tipo de ecuaciones sirve como ejercicio para familiarizase con las propiedades de las potencias y las propiedades de los logaritmos.
En este tipo de ecuaciones, es conveniente reescribir las expresiones involucradas para cancelar la base con el argumento, es por esto que descomponemos los números involucrados como productos de factores primos. Entonces,

De esta forma, podemos aplicar la propiedad del logaritmo que nos permite sacar el exponente del argumento como un factor que multiplica el logaritmo, es decir,

Notamos inmediatamente que logaritmo base dos de dos es igual a uno, es decir, 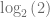 . Por lo tanto, concluimos que
. Por lo tanto, concluimos que

Ejemplo 2
Calcule la solución de la siguiente ecuación logarítmica:
![\log_{25} \left( \sqrt[4]{5} \right) = x](https://s0.wp.com/latex.php?latex=%5Clog_%7B25%7D+%5Cleft%28+%5Csqrt%5B4%5D%7B5%7D+%5Cright%29+%3D+x&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Si bien podemos calcular ![\log_{25} \left( \sqrt[4]{5} \right)](https://s0.wp.com/latex.php?latex=%5Clog_%7B25%7D+%5Cleft%28+%5Csqrt%5B4%5D%7B5%7D+%5Cright%29&bg=ffffff&fg=5e5e5e&s=0&c=20201002) directamente con una calculadora, este tipo de ecuaciones sirve como ejercicio para familiarizase con las propiedades de las potencias y las propiedades de los logaritmos.
directamente con una calculadora, este tipo de ecuaciones sirve como ejercicio para familiarizase con las propiedades de las potencias y las propiedades de los logaritmos.
En este tipo de ecuaciones, es conveniente reescribir las expresiones involucradas para cancelar la base con el argumento. Entonces, conviene reescribir ![\sqrt[4]{5}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B4%5D%7B5%7D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) como
como 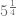 y así,
y así,

De esta forma, podemos aplicar la propiedad del logaritmo que nos permite sacar el exponente del argumento como un factor que multiplica el logaritmo, es decir,

Notamos además, que  se puede reescribir como
se puede reescribir como 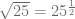 , por lo tanto
, por lo tanto

sacamos nuevamente el exponente del argumento como un factor que multiplica el logaritmo,

Notamos inmediatamente que logaritmo base dos de dos es igual a uno, es decir, 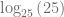 . Por lo tanto, concluimos que
. Por lo tanto, concluimos que

Ejemplo 3
Calcule la solución de la siguiente ecuación logarítmica:

Si bien podemos calcular  directamente con una calculadora, este tipo de ecuaciones sirve como ejercicio para familiarizase con las propiedades de las potencias y las propiedades de los logaritmos.
directamente con una calculadora, este tipo de ecuaciones sirve como ejercicio para familiarizase con las propiedades de las potencias y las propiedades de los logaritmos.
En este tipo de ecuaciones, es conveniente reescribir las expresiones involucradas para cancelar la base con el argumento. Entonces, conviene reescribir 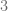 como
como  y así,
y así,
De esta forma, podemos aplicar la propiedad del logaritmo que nos permite sacar el exponente del argumento como un factor que multiplica el logaritmo, es decir,

Notamos inmediatamente que logaritmo base dos de dos es igual a uno, es decir,  . Por lo tanto, concluimos que
. Por lo tanto, concluimos que
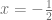
Ejemplo 4
Calcule la solución de la siguiente ecuación logarítmica:

Si bien podemos calcular  directamente con una calculadora, este tipo de ecuaciones sirve como ejercicio para familiarizase con las propiedades de las potencias y las propiedades de los logaritmos.
directamente con una calculadora, este tipo de ecuaciones sirve como ejercicio para familiarizase con las propiedades de las potencias y las propiedades de los logaritmos.
En este tipo de ecuaciones, es conveniente reescribir las expresiones involucradas para cancelar la base con el argumento. Entonces, conviene reescribir  como
como  y así,
y así,
De esta forma, podemos aplicar la propiedad del logaritmo que nos permite sacar el exponente del argumento como un factor que multiplica el logaritmo, es decir,

Notamos inmediatamente que logaritmo base dos de dos es igual a uno, es decir,  . Por lo tanto, concluimos que
. Por lo tanto, concluimos que
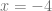
Veamos en lo siguientes ejemplos como aplicar las propiedades de los logaritmos para calcular la solución de algunas ecuaciones exponenciales.
Ejemplos
Ejemplo 5
Calcule la solución de la siguiente ecuación exponencial:

Lo primero que debemos notar es que las bases de los elementos involucrados no son iguales, así que el procedimiento no es tan simple como igualar los exponentes.
Una de las técnicas para abordar este tipo de ecuaciones es aplicar el logaritmo con la base que más convenga en ambos lados de la ecuación. En este caso, aplicamos el logaritmo base tres pues esta es la base que involucra a la incógnita. Entonces,
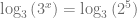
De esta forma, podemos aplicar la propiedad del logaritmo que nos permite sacar el exponente del argumento como un factor que multiplica el logaritmo, es decir,
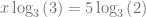
Notamos inmediatamente que el logaritmo cuya base es la misma que el argumento igual a uno, es decir,  . Por lo tanto, concluimos que
. Por lo tanto, concluimos que

Para calcular el valor de  es necesario recurrir a una calculadora científica. Usualmente, las calculadoras científicas sólo permiten calcular el logaritmo base diez o el logaritmo neperiano (base
es necesario recurrir a una calculadora científica. Usualmente, las calculadoras científicas sólo permiten calcular el logaritmo base diez o el logaritmo neperiano (base  ). Sin, embargo, usando la propiedad cambio de base, podemos calcular este logaritmo, pues
). Sin, embargo, usando la propiedad cambio de base, podemos calcular este logaritmo, pues

Por lo tanto,

Ejemplo 6
Calcule la solución de la siguiente ecuación exponencial:
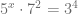
Lo primero que debemos notar es que las bases de los elementos involucrados no son iguales, así que el procedimiento no es tan simple como igualar los exponentes.
Una de las técnicas para abordar este tipo de ecuaciones es aplicar el logaritmo con la base que más convenga en ambos lados de la ecuación. En este caso, aplicamos el logaritmo base cinco pues esta es la base que involucra a la incógnita. Entonces,
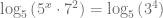
Entonces, aplicamos la propiedad del logaritmo que nos permite separar el producto del argumento como una suma de logaritmos, es decir,
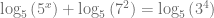
De esta forma, podemos aplicar la propiedad del logaritmo que nos permite sacar el exponente del argumento como un factor que multiplica el logaritmo, es decir,
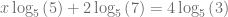
Notamos inmediatamente que el logaritmo cuya base es la misma que el argumento igual a uno, es decir,  . Por lo tanto,
. Por lo tanto,
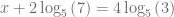
Posteriormente, despejamos la incógnita  para concluir que
para concluir que

Para calcular el valor de  es necesario recurrir a una calculadora científica. Usualmente, las calculadoras científicas sólo permiten calcular el logaritmo base diez o el logaritmo neperiano (base
es necesario recurrir a una calculadora científica. Usualmente, las calculadoras científicas sólo permiten calcular el logaritmo base diez o el logaritmo neperiano (base  ). Sin, embargo, usando la propiedad cambio de base, podemos calcular estos logaritmo, pues
). Sin, embargo, usando la propiedad cambio de base, podemos calcular estos logaritmo, pues
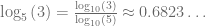
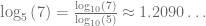
Por lo tanto,
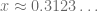
and
are two real numbers, the conjugate of the sum
is defined as
. Similarly, the conjugate of the subtraction
is defined as
. That is, the sign between the two is changed. The importance of the conjugate lies in the fact that the product of an addition by its conjugate is equal to a difference of squares, that is,


. It does not have much sense to identify the conjugate of this expression because we can simply make the subtraction and obtain 7 as a result.
. Note that one of the involved sums is the square root of twelve, so it cannot be subtracted with five, so we conclude that its conjugate is
.
. Note that one of the summands involved is the square root of eight, so it cannot be added with three, so we conclude that its conjugate is
.
. Note that one of the sums involved is three multiplied by one unknown, so it cannot be subtracted with seven, then, we conclude that its conjugate is
.
. Let’s notice that one of the involved sums is four multiplied by one unknown, therefore it cannot be added with 15, then, we conclude that its conjugate is
.
. This subtraction cannot be done, so we conclude that your conjugate is
. Noting that the sign inside the root does not change.

























Debe estar conectado para enviar un comentario.