- La jerarquía de las operaciones
- Ejemplos
- Ejemplo 1
- Ejemplo 2
- Ejemplo 3
- Ejemplo 4
- Ejemplo 5
- Ejemplo 6
- Los signos de agrupación
- Ejemplos
- Ejemplo 7
- Ejemplo 8
- Ejemplo 9
- Ejemplo 10
- Ejemplo 11
- Ejemplo 12
¿Qué es saber sumar, restar, multiplicar y dividir? Si bien, durante los estudios básicos de matemáticas aprendemos a efectuar cualquiera de las operaciones básicas, es poco lo que se indaga cuando estas operaciones se encuentran combinadas.
También pudiera interesarte
La jerarquía de las operaciones
Al efectuar distintas operaciones entre números reales, resulta necesario especificar el orden en el que se deben efectuar las operaciones, esto es para evitar ambigüedades la hora de expresar los resultados. Entonces, si consideramos las operaciones de suma, resta, multiplicación y división; el orden en el que estas deben efectuarse es el siguiente:
Es decir, primero se efectúan todos los productos, después todas las divisiones, después todas las sumas y por último, todas las restas.
La suma será expresada con una cruz (  ). La resta será expresada con una raya horizontal (
). La resta será expresada con una raya horizontal (  ). El producto o multiplicación será expresado con un punto (
). El producto o multiplicación será expresado con un punto (  ), aunque también se puede expresar con dos rayas cruzadas (
), aunque también se puede expresar con dos rayas cruzadas (  ). La división será expresada con dos puntos y una raya horizontal (
). La división será expresada con dos puntos y una raya horizontal ( 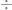 ) que denota un número sobre otro número, aunque también se puede expresar simplemente con dos puntos (
) que denota un número sobre otro número, aunque también se puede expresar simplemente con dos puntos (  ) o con una barra vertical (
) o con una barra vertical ( 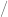 ).
).
Veamos en lo siguientes ejemplos como aplicar esta jerarquía de las operaciones al toparnos con expresiones que cuentan con distintas operaciones.
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ejemplos
Ejemplo 1
Calcule el resultado de la siguiente siguiente expresión matemática

En esta ocasión encontramos un producto y una suma. La jerarquía de las operaciones indica que primero debemos efectuar el producto, de esta forma, obtenemos
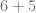
Posteriormente, efectuamos la suma y concluimos que el resultado será

Ejemplo 2
Calcule el resultado de la siguiente siguiente expresión matemática
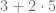
En esta ocasión encontramos un producto y una suma. Notemos que a diferencia del ejemplo anterior, la suma aparece primero, sin embargo, la jerarquía de las operaciones indica que primero debemos efectuar el producto, de esta forma, obtenemos

Finalmente, efectuamos la suma y concluimos que el resultado será
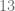
Ejemplo 3
Calcule el resultado de la siguiente siguiente expresión matemática
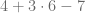
En esta ocasión encontramos un producto, una suma y una resta. La jerarquía de las operaciones indica que primero debemos efectuar el producto, de esta forma, obtenemos
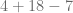
Posteriormente, efectuamos la suma,

Finalmente, efectuamos la resta
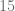
Ejemplo 4
Calcule el resultado de la siguiente siguiente expresión matemática

En esta ocasión encontramos un producto, una suma y una resta. La jerarquía de las operaciones indica que primero debemos efectuar la división, de esta forma, obtenemos

Posteriormente, efectuamos las sumas,

Finalmente, efectuamos la resta

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ejemplo 5
Calcule el resultado de la siguiente siguiente expresión matemática
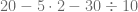
En esta ocasión encontramos un producto, una división y dos resta. La jerarquía de las operaciones indica que primero debemos efectuar el producto, de esta forma, obtenemos

Posteriormente, efectuamos la división,
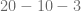
En este caso, notamos que hay dos restas, entonces agrupamos las restas y las efectuamos
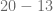
Finalmente, efectuamos la resta
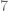
Ejemplo 6
Calcule el resultado de la siguiente siguiente expresión matemática
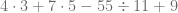
En esta ocasión encontramos dos productos, una división, dos sumas y una resta. La jerarquía de las operaciones indica que primero debemos efectuar los productos, de esta forma, obtenemos

Posteriormente, efectuamos la división,
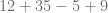
En este caso, notamos que hay más de dos números sumando, entonces agrupamos las sumas

Posteriormente, efectuamos las sumas

Finalmente, efectuamos la resta
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Los signos de agrupación
Hay expresiones en las que las jerarquía de las operaciones no basta para calcular un resultado, pues puede no estar muy claro cual es la operación que debe efectuarse. Por ejemplo, si consideramos la expresión
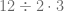
La jerarquía de las operaciones indica que primero debe efectuarse el producto, sin embargo, ¿es correcto multiplicar un número entero por un divisor? ¿Es correcto efectuar primero la división y después el producto? ¿Es correcto multiplicar el doce por el tres? No queda claro como efectuar esta operación correctamente.
Considerando esto, debemos definir una nueva herramienta que indique con claridad cuales son las operaciones que se deben efectuar primero, que llamaremos signos de agrupación.
Usaremos paréntesis 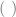 para agrupar las operaciones que se deben efectuar antes de efectuar cualquier otra operación. De esta forma, si consideramos la operación
para agrupar las operaciones que se deben efectuar antes de efectuar cualquier otra operación. De esta forma, si consideramos la operación

Se está indicando que primero se debe efectuar el producto  , para obtener
, para obtener  que a su vez, es igual a
que a su vez, es igual a 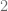 . Por otra parte, si consideramos la operación
. Por otra parte, si consideramos la operación
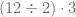
Se está indicando que primero se debe efectuar la división  , para obtener
, para obtener  que a su vez, es igual a
que a su vez, es igual a  .
.
Notemos que ambos casos arrojan resultados distintos, ahí radica la importancia del uso de los paréntesis para agrupar las operaciones que se deben efectuar primero.
También puede ocurrir que debemos agrupar operaciones que entre números que ya están agrupados por otras operaciones, para esto usamos otros signos de agrupación: corchetes ![[ \ ]](https://s0.wp.com/latex.php?latex=%5B+%5C+%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) y llaves
y llaves  , sobre los cuales también definimos una jerarquía.
, sobre los cuales también definimos una jerarquía.
Es decir, primero se efectúan todas las operaciones que se encuentran entre paréntesis, después todas las operaciones que se encuentran entre corchetes y por último, todas las operaciones que se encuentran entre llaves.
Veamos en lo siguientes ejemplos como aplicar esta jerarquía de las operaciones y los signos de agrupación al toparnos con expresiones que cuentan con distintas operaciones.
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ejemplos
Ejemplo 7
Calcule el resultado de la siguiente siguiente expresión matemática

Lo primero que debemos notar es que la suma  está encerrada en un paréntesis. La jerarquía de los signos de agrupación indica que primero debemos efectuar las operaciones que están dentro de los paréntesis, de esta forma, obtenemos
está encerrada en un paréntesis. La jerarquía de los signos de agrupación indica que primero debemos efectuar las operaciones que están dentro de los paréntesis, de esta forma, obtenemos

Finalmente, efectuamos el producto,

Ejemplo 8
Calcule el resultado de la siguiente siguiente expresión matemática
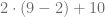
Lo primero que debemos notar es que la resta  está encerrada en un paréntesis. La jerarquía de los signos de agrupación indica que primero debemos efectuar las operaciones que están dentro de los paréntesis, de esta forma, obtenemos
está encerrada en un paréntesis. La jerarquía de los signos de agrupación indica que primero debemos efectuar las operaciones que están dentro de los paréntesis, de esta forma, obtenemos
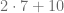
La jerarquía de las operaciones indica que primero debemos efectuar el producto, de esta forma, obtenemos

Finalmente, efectuamos la suma,
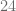
Ejemplo 9
Calcule el resultado de la siguiente siguiente expresión matemática
![3 + 4 \cdot [ 24 \div (2+6) + 5]](https://s0.wp.com/latex.php?latex=3+%2B+4+%5Ccdot+%5B+24+%5Cdiv+%282%2B6%29+%2B+5%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Debemos notar que hay dos signos de agrupación: paréntesis y corchetes. Esto se debe hay que agrupaciones de operaciones dentro de agrupaciones de operaciones.
La jerarquía de los signos de agrupación indica que primero debemos efectuar las operaciones que están dentro de los paréntesis, de esta forma, obtenemos
![3 + 4 \cdot [ 24 \div 8 + 5]](https://s0.wp.com/latex.php?latex=3+%2B+4+%5Ccdot+%5B+24+%5Cdiv+8+%2B+5%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Posteriormente, efectuamos las operaciones que se encuentran dentro de los corchetes. La jerarquía de las operaciones indica que primero debemos efectuar la división, obteniendo
![3 + 4 \cdot [3 + 5]](https://s0.wp.com/latex.php?latex=3+%2B+4+%5Ccdot+%5B3+%2B+5%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Posteriormente, efectuamos la suma que se encuentra dentro de los corchetes,
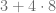
Posteriormente, efectuamos el producto,

Posteriormente, efectuamos la suma,
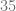
Ejemplo 10
Calcule el resultado de la siguiente siguiente expresión matemática
![100 - 2 \cdot \big[ (10 + 20) \div 15 - 5 \cdot (12 - 3) \big]](https://s0.wp.com/latex.php?latex=100+-+2+%5Ccdot+%5Cbig%5B+%2810+%2B+20%29+%5Cdiv+15+-+5+%5Ccdot+%2812+-+3%29+%5Cbig%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Debemos notar que hay dos signos de agrupación: paréntesis y corchetes. Esto se debe hay que agrupaciones de operaciones dentro de agrupaciones de operaciones.
La jerarquía de los signos de agrupación indica que primero debemos efectuar las operaciones que están dentro de los paréntesis, de esta forma, obtenemos
![100 - 2 \cdot [ 30 \div 15 - 5 \cdot 9 ]](https://s0.wp.com/latex.php?latex=100+-+2+%5Ccdot+%5B+30+%5Cdiv+15+-+5+%5Ccdot+9+%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Posteriormente, efectuamos las operaciones que se encuentran dentro de los corchetes. La jerarquía de las operaciones indica que primero debemos efectuar el producto e incluso, en este caso podemos efectuar la división en el mismo paso sin que se altere el resultado, obteniendo
![100 - 2 \cdot [ 2 - 45 ]](https://s0.wp.com/latex.php?latex=100+-+2+%5Ccdot+%5B+2+-+45+%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Posteriormente, efectuamos la resta que se encuentra dentro de los corchetes,
![100 - 2 \cdot [ -43 ]](https://s0.wp.com/latex.php?latex=100+-+2+%5Ccdot+%5B+-43+%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Posteriormente, efectuamos el producto y aplicando la ley de los signos, tenemos

Posteriormente, efectuamos la suma,

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ejemplo 11
Calcule el resultado de la siguiente siguiente expresión matemática
![5 - \{ 20 + 35 \div [17 - (3+7) + 25 \div (3+2) - 2] \}](https://s0.wp.com/latex.php?latex=5+-+%5C%7B+20+%2B+35+%5Cdiv+%5B17+-+%283%2B7%29+%2B+25+%5Cdiv+%283%2B2%29+-+2%5D+%5C%7D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Debemos notar que hay tres signos de agrupación: paréntesis, corchetes y llaves. Esto se debe hay que agrupaciones de operaciones dentro de agrupaciones de operaciones.
La jerarquía de los signos de agrupación indica que primero debemos efectuar las operaciones que están dentro de los paréntesis, de esta forma, obtenemos
![5 - \{ 20 + 35 \div [17 - 10 + 25 \div 5 - 5] \}](https://s0.wp.com/latex.php?latex=5+-+%5C%7B+20+%2B+35+%5Cdiv+%5B17+-+10+%2B+25+%5Cdiv+5+-+5%5D+%5C%7D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Posteriormente, efectuamos las operaciones que se encuentran dentro de los corchetes. La jerarquía de las operaciones indica que primero debemos efectuar la división, obteniendo
![5 - \{ 20 + 35 \div [17 - 10 + 5 - 5] \}](https://s0.wp.com/latex.php?latex=5+-+%5C%7B+20+%2B+35+%5Cdiv+%5B17+-+10+%2B+5+-+5%5D+%5C%7D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Posteriormente, agrupamos las sumas dentro de los corchetes
![5 - \{ 20 + 35 \div [17 + 5 - 10 - 5] \}](https://s0.wp.com/latex.php?latex=5+-+%5C%7B+20+%2B+35+%5Cdiv+%5B17+%2B+5+-+10+-+5%5D+%5C%7D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Posteriormente, efectuamos las sumas que se encuentra dentro de los corchetes e incluso, en este caso podemos efectuar las restas en el mismo paso sin que se altere el resultado
![5 - \{ 20 + 35 \div [22 - 15] \}](https://s0.wp.com/latex.php?latex=5+-+%5C%7B+20+%2B+35+%5Cdiv+%5B22+-+15%5D+%5C%7D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Posteriormente, efectuamos la resta,
![5 - \{ 20 + 35 \div [7] \}](https://s0.wp.com/latex.php?latex=5+-+%5C%7B+20+%2B+35+%5Cdiv+%5B7%5D+%5C%7D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Posteriormente, efectuamos la división,

Posteriormente, efectuamos la suma,

Posteriormente, efectuamos la suma,

Finalmente, efectuamos la resta,
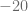
Ejemplo 12
Calcule el resultado de la siguiente siguiente expresión matemática
![72 + \cdot \{ -30 + 5 \cdot [4 + 2 \cdot (5-2) - 3 \cdot (1+4) - 2] \} \div [ 3 \cdot (10 - 7) ]](https://s0.wp.com/latex.php?latex=72+%2B+%5Ccdot+%5C%7B+-30+%2B+5+%5Ccdot+%5B4+%2B+2+%5Ccdot+%285-2%29+-+3+%5Ccdot+%281%2B4%29+-+2%5D+%5C%7D+%5Cdiv+%5B+3+%5Ccdot+%2810+-+7%29+%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Debemos notar que hay tres signos de agrupación: paréntesis, corchetes y llaves. Esto se debe hay que agrupaciones de operaciones dentro de agrupaciones de operaciones.
La jerarquía de los signos de agrupación indica que primero debemos efectuar las operaciones que están dentro de los paréntesis, de esta forma, obtenemos
![72 + \{ -30 + 5 \cdot [4 + 2 \cdot 3 - 3 \cdot 5 - 2] \} \div [ 3 \cdot 3 ]](https://s0.wp.com/latex.php?latex=72+%2B+%5C%7B+-30+%2B+5+%5Ccdot+%5B4+%2B+2+%5Ccdot+3+-+3+%5Ccdot+5+-+2%5D+%5C%7D+%5Cdiv+%5B+3+%5Ccdot+3+%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Posteriormente, efectuamos las operaciones que se encuentran dentro de los corchetes. La jerarquía de las operaciones indica que primero debemos efectuar los productos, obteniendo
![72 + \{ -30 + 5 \cdot [4 + 6 - 15 - 2] \} \div [ 9 ]](https://s0.wp.com/latex.php?latex=72+%2B+%5C%7B+-30+%2B+5+%5Ccdot+%5B4+%2B+6+-+15+-+2%5D+%5C%7D+%5Cdiv+%5B+9+%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Posteriormente, efectuamos las sumas que se encuentra dentro de los corchetes e incluso, en este caso podemos efectuar las restas en el mismo paso sin que se altere el resultado
![72 + \{ -30 + 5 \cdot [10 - 17] \} \div [ 9 ]](https://s0.wp.com/latex.php?latex=72+%2B+%5C%7B+-30+%2B+5+%5Ccdot+%5B10+-+17%5D+%5C%7D+%5Cdiv+%5B+9+%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Posteriormente, efectuamos la resta que se encuentra dentro de los corchetes,
![72 + \{ -30 + 5 \cdot [-3] \} \div [ 9 ]](https://s0.wp.com/latex.php?latex=72+%2B+%5C%7B+-30+%2B+5+%5Ccdot+%5B-3%5D+%5C%7D+%5Cdiv+%5B+9+%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Posteriormente, efectuamos el producto que se encuentra dentro de las llaves,
![72 + \{ -30 - 15 \} \div [ 9 ]](https://s0.wp.com/latex.php?latex=72+%2B+%5C%7B+-30+-+15+%5C%7D+%5Cdiv+%5B+9+%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Posteriormente, efectuamos la resta que se encuentra dentro de las llaves,
![72 + \{ -45 \} \div [ 9 ]](https://s0.wp.com/latex.php?latex=72+%2B+%5C%7B+-45+%5C%7D+%5Cdiv+%5B+9+%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Posteriormente, efectuamos la división,
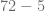
Finalmente, efectuamos la resta,

Ps, considerando los costos de producción, le parece que este precio es generoso para usted por lo que decide proveer al supermercado con
kilos de tomate. La semana siguiente vuelve al supermercado y ve que un kilo de tomates tiene un precio de
Ps, considerando que está en la mitad del precio de la semana anterior, usted decide proveer al supermercado con
kilos de tomate.
y la variable cantidad, denotada por
; para mantener la simplicidad de los modelos, consideraremos una economía simple, es decir, tal que las variables
y
sólo pueden tener valores positivos. De esta forma, nos ubicaremos sólo en el primer cuadrante del plano cartesiano.

kilos cuando el precio es de
Ps. por kilo, y de
kilos cuando el precio es de
Ps. por kilo. ¿Cuál es la ecuación general de la recta que define la relación entre el precio y la oferta? ¿Cuál será la cantidad ofertada si fija el precio en
Ps.?
kilos cuando el precio es de
Ps., podemos representar esta información como un punto
el plano cartesiano donde
y
, es decir, el punto
; de igual forma, si la oferta es de
kilos cuando el precio es de
Ps., podemos representar esta información con el punto
.
y
son dos puntos en el plano cartesiano, calculamos el valor de la pendiente,
y
es llamada la Ecuación de Oferta de zanahoria. Este tipo de ecuaciones siempre tendrá pendiente positiva y su gráfica será una recta creciente.

Ps. debemos considerar la ecuación de oferta y sustituir el valor
en ella, posteriormente se despeja la variable
, de la siguiente forma
kilos semanales si se fija el precio en
Ps.
pares cuando el precio es de
Ps. por par, y de
pares cuando el precio es de
Ps. por par. ¿Cuál es la ecuación general de la recta que define la relación entre el precio y la oferta? ¿Cuál será la cantidad ofertada si fija el precio en
Ps.?
pares cuando el precio es de
Ps., podemos representar esta información con el punto
; de igual forma, si la oferta es de
pares cuando el precio es de
Ps., podemos representar esta información con el punto
.
y
son dos puntos en el plano cartesiano, calculamos el valor de la pendiente,
y
es llamada la Ecuación de Oferta de zapatos para dama. Este tipo de ecuaciones siempre tendrá pendiente negativa y su gráfica será una recta decreciente.

Ps. debemos considerar la ecuación de oferta y sustituir el valor
en ella, posteriormente se despeja la variable
, de la siguiente forma
pares mensuales si se fija el precio en
Ps.
, cualquier ecuación de oferta tiene la forma












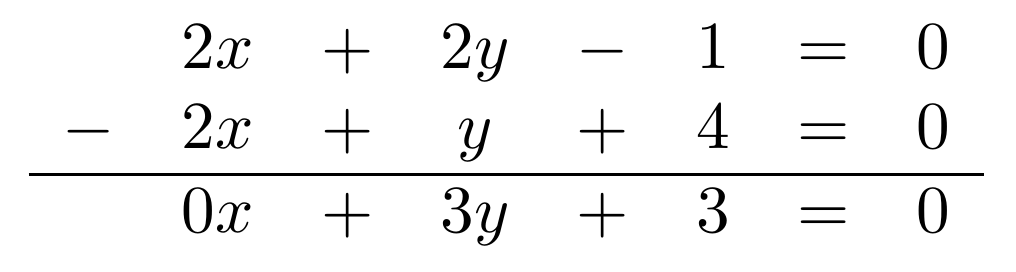
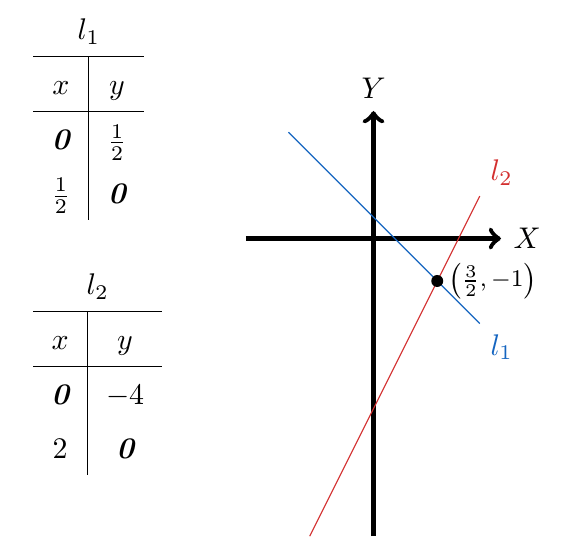
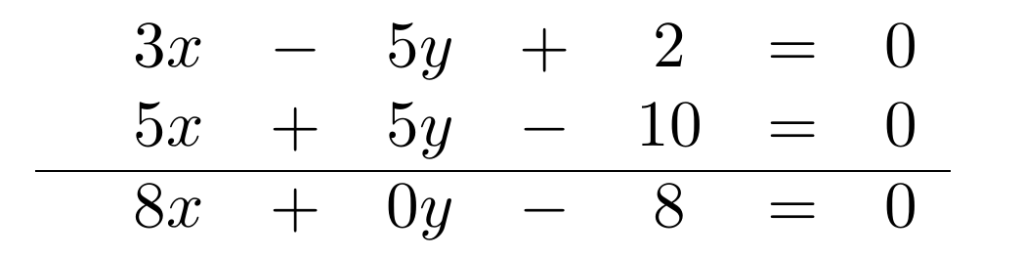
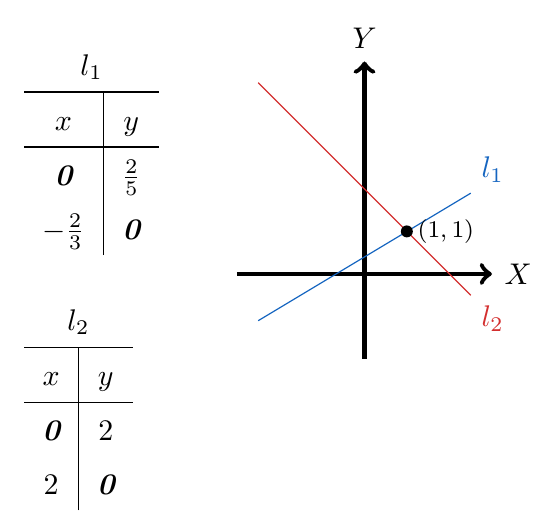
Debe estar conectado para enviar un comentario.