R: Diagrama de Dispersión

06.05.202107.12.2022 Anthonny Arias-García5 comentarios

Antes de empezar a definir un modelo sobre un conjunto de datos, es importante conocer el comportamiento de una variable respecto a otra pues de esta forma, podemos hacernos una idea de cual es el modelo más adecuado para describirlo.

También pudiera interesarte

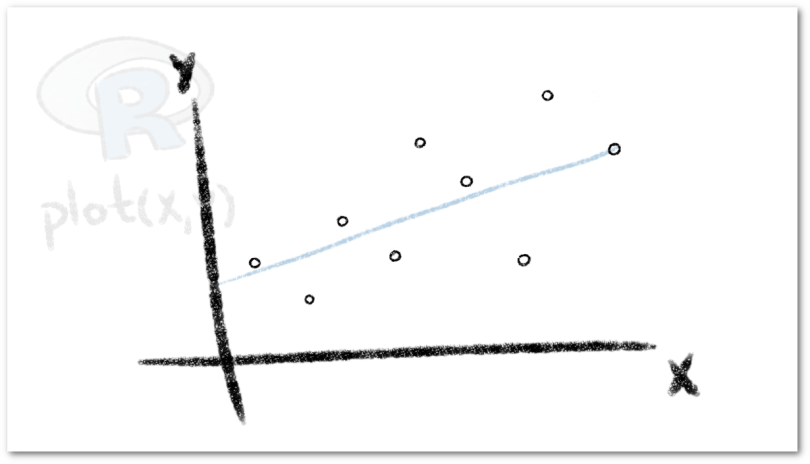
Diagrama de Dispersión

Una de las formas más directas y sencillas para estudiar la forma en que se relacionan dos variables es usando un diagrama de dispersión. Si consideramos dos variables de un conjunto de datos, digamos una variable exógena x y una variable endógena y, un Diagrama de Dispersión (o Gráfico de Dispersión) consiste en ubicar en el plano cartesiano cada par ordenado formado por los elementos de estas dos variables. Ubicando la variable exógena en el eje horizontal y la variable endógena en el eje vertical.

De esta forma, si nuestro objetivo es definir un Modelo de Regresión Lineal, ubicamos en el eje horizontal, los valores de la variable $X$ y en el eje vertical, los valores de la variable $Y$ . Podemos generar un diagrama de dispersión en R recurriendo a la instrucción plot y usamos la siguiente sintaxis:

plot(X,Y)

Ejemplo

Consideremos un pequeño conjunto de datos, particularmente, los datos que se encuentran en la Tabla 3.2 del libro de Econometría de Damodar N. Gujarati and Dawn Porter en su quinta edición. Este conjunto de datos proporciona los datos primarios que se necesitan para estimar el efecto cuantitativo de la escolaridad en los salarios:

Observación	Salario	Escolaridad
1	4.4567	6
2	5.77	7
3	5.9787	8
4	7.3317	9
5	7.3182	10
6	6.5844	11
7	7.8182	12
8	7.8351	13
9	11.0223	14
10	10.6738	15
11	10.8361	16
12	13.615	17
13	13.531	18

Tabla 3.2

Para generar un diagrama de dispersión que nos ayude a estudiar como el nivel de estudios afecta el salario de una persona, entonces: la variable Escolaridad será nuestra variable exógena y será ubicada en el eje horizontal; la variable Salario será nuestra variable endógena y será ubicada en el eje vertical.

Recurriremos a la instrucción plot para generar un diagrama de dispersión y usamos la siguiente sintaxis:

plot(escolaridad,salario)

Al ejecutar esta instrucción, aparecerá de forma inmediata el siguiente gráfico:

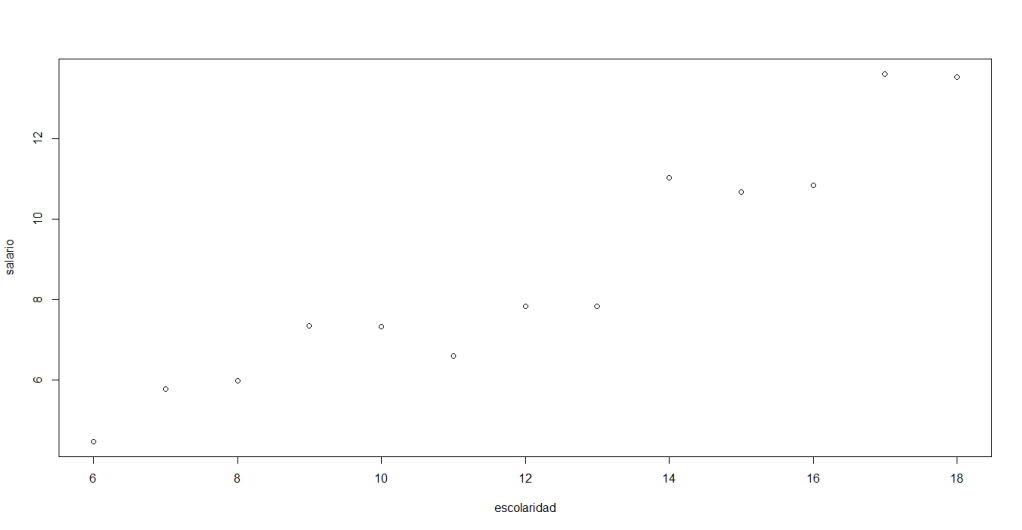
En su pantalla debería aparecer lo siguiente:

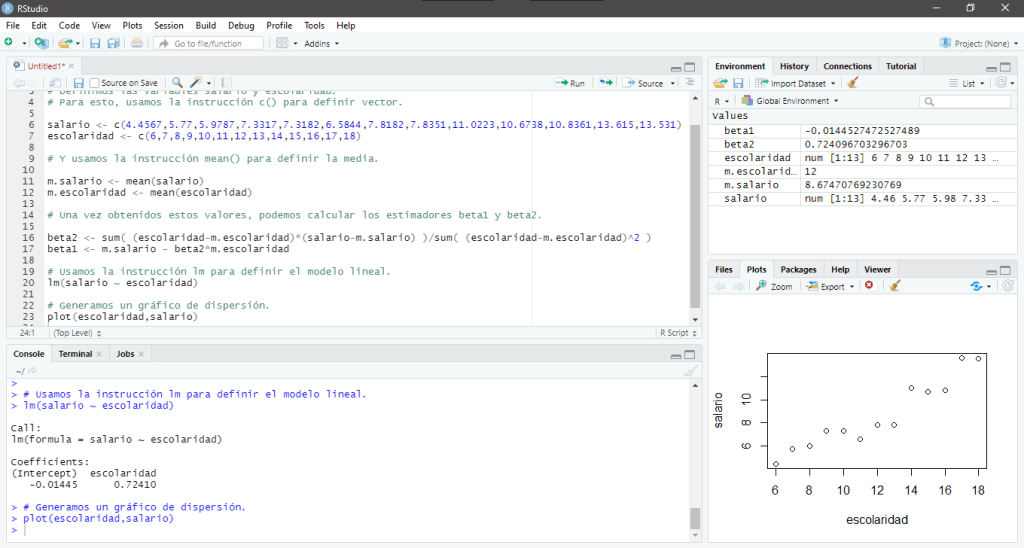
También es posible dibujar sobre el diagrama de dispersión la Recta de Regresión, para esto recurrimos a la instrucción abline(), usamos la siguiente sintaxis para generar la recta definida por $\hat{Y} = \hat{\beta}_1 + \hat{\beta}_2 X$:

abline(lm(Y ~ X))

Anuncios

Ejemplo para los residuos

Si bien los diagramas de dispersión nos ayudan a estudiar el comportamiento de dos variables, también nos ayudan a estudiar el comportamiento de los residuos. Uno de los supuestos para del Modelo Clásico de Regresión Lineal, estipula que no debe haber autocorrelación, esto quiere decir que la correlación de los residuos debe ser nula.

A partir de la forma en que está definido el modelo lineal, podemos calcular los residuos usando la siguiente fórmula:

$\hat{u}_i = Y_i - \hat{Y}_i$

Entonces, si calculamos cada uno de los valores estimados $\hat{Y}_i$ , podemos determinar los residuos usando la siguiente sintaxis:

Y.e <- beta1 + beta2*X
res <- Y - Y.e

Usamos la instrucción plot(res) para generar un gráfico de dispersión de los residuos tomando en cuenta que en el eje horizontal se ubica el número de observación y en el vertical el residuo correspondiente. Un indicador de no autocorrelación es que el gráfico de dispersión no presente ningún patrón de comportamiento, en términos coloquiales: que estén todos a lo loco.

Continuando con nuestro ejemplo, generamos un gráfico usando la siguiente sintaxis:

salario.e <- beta1 + beta2*escolaridad
residuos <- salario - salario.e
plot(residuos)

Al ejecutar estas instrucciones, aparecerá de forma inmediata el siguiente gráfico:

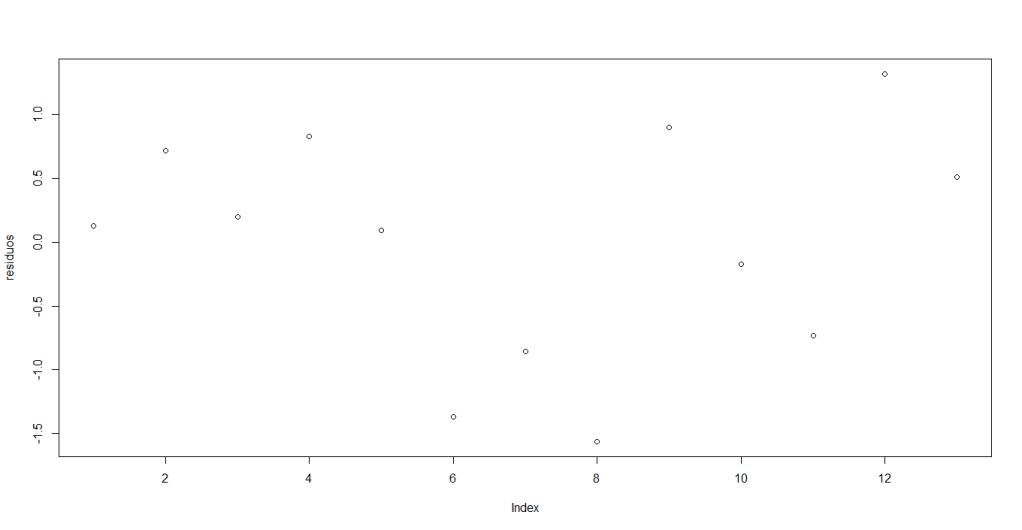
Diagrama de Dispersión de los Residuos | totumat.com

En su pantalla debería aparecer:

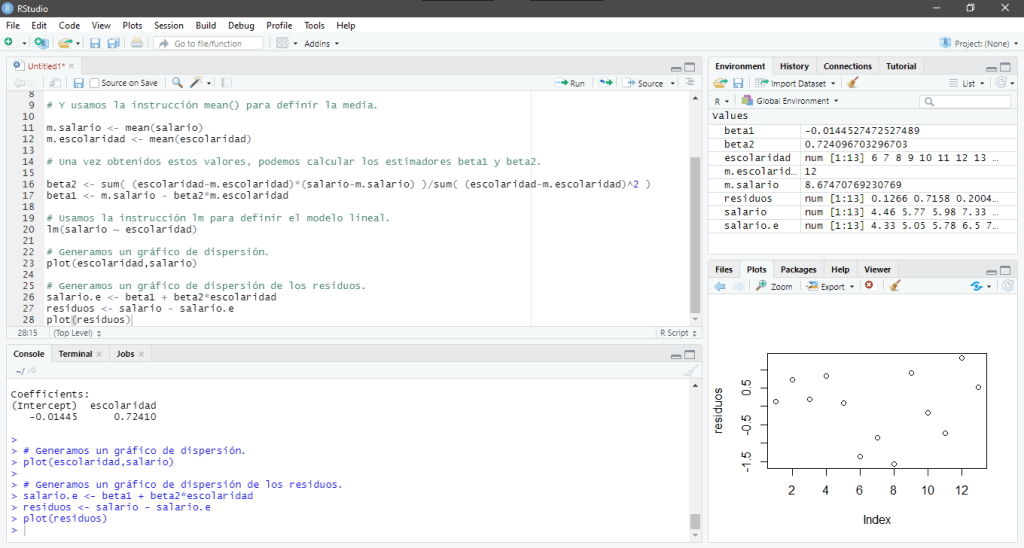
Aunque pareciera no haber ningún patrón, no podemos asegurar no hay autocorrelación, también hay que considerar que el tamaño de la muestra es pequeño así que las afirmaciones que se hagan sobre el comportamiento que describe el modelo lineal puede ser impreciso.

Verbos para redactar competencias

03.05.202118.06.2024 Anthonny Arias-García2 comentarios

Información importante: Esta tabla de verbos es de uso personal, no constituye una guía profesional para la estructuración de programas por competencias. Sin embargo, la comparto para el que necesite tener a la mano una lista de verbos cuando esté redactando. Dicho esto, es importante tener algunas consideraciones a la hora de redactar competencias:

La conjugación de los verbos para redactar competencias debe hacerse en tiempo presente en tercera persona, por ejemplo: elige, resuelve, comparte.

Considerando que los verbos deben conjugarse, se contraindica la forma infinitiva de estos verbos, por ejemplo, no debe usar: elegir, resolver, compartir.

Las capacidades conceptuales son las relacionadas con el saber teórico, el conocimiento y el «saber profesional».

Las capacidades procedimentales son las relacionadas con el saber práctico, metodológico y el «hacer profesional».

Las capacidades actitudinales son las relacionadas con: saber social, actitud, valor y el «ser profesional».

También pudiera interesarte

Contenidos Conceptuales

Analizar
Comprobar
Deducir
Definir
Demostrar
Describir
Diferenciar
Elegir
Enumerar
Evaluar
Explicar
Expresar
Identificar
Inducir
Interpretar
Localizar
Memorizar
Planear
Reconocer
Reconocer
Recordar
Relacionar
Sintetizar

Contenidos Procedimentales

Adaptar
Caracterizar
Clasificar
Construir
Controlar
Conversar
Crear
Desarrollar
Determinar
Diseñar
Efectuar
Expresar
Formar
Investigar
Manejar
Manipular
Observar
Operar
Organizar
Orientarse
Programar
Proyectar
Recoger
Representar
Resolver
Simular
Solucionar
Usar
Utilizar

Contenidos Actitudinales

Aceptar
Admirar
Apreciar
Asumir
Autoestimar
Colaborar
Compartir
Contemplar
Crear
Cuidar
Disfrutar
Integrar
Interesar
Interiorizar
Inventar
Mostrar
Participar
Preferir
Rechazar
Respetar
Tender a
Valorar

Esta lista está basada en el trabajo de la Catedrática Xiomara Ortega, pero pareciera que ha sido un trabajo descontinuado y aunque hay varias observaciones hechas sobre su trabajo, pocas han sido las correcciones, en consecuencia agradezco cualquier corrección u observación que pueda mejorar o complementar el contenido de esta publicación.

Bibliografía Consultada:

perfil, V. (2013). Lista de verbos para redactar competencias.. Xjog60.blogspot.com. Retrieved 3 May 2021, from http://xjog60.blogspot.com/2013/01/lista-de-verbos-para-redactar.html
(2021). Miguelangel13.files.wordpress.com. Retrieved 3 May 2021, from https://miguelangel13.files.wordpress.com/2010/02/verbos-para-redactar-competencias.pdf
(2021). Paho.org. Retrieved 3 May 2021, from https://www.paho.org/hq/dmdocuments/2010/dco-base-redactar-competencias-INSP.pdf

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.

La Curva de Lorenz y el Coeficiente de Gini

01.05.202107.09.2025 Anthonny Arias-García1 comentario

Una vez que se determina el Producto Interno Bruto de un país, ¿qué cantidad de este dinero le corresponde a cada ciudadano? Independientemente de cómo esté distribuida la riqueza entre los habitantes de un país, por distintas razones (justas o no), esta distribución no es equitativa, de ahí radica la importancia de presentar un modelo matemático que permita describir esta distribución.

También pudiera interesarte

La Curva de Lorenz

La Curva de Lorenz es una función que permite describir la distribución de la riqueza de en un país y también es conocida como la Línea de Desigualdad Perfecta. Usualmente esta se denota como $L(x)$ . En términos porcentuales, establece una correspondencia entre el porcentaje acumulado de ingresos y el porcentaje acumulado de la población receptora de ingresos, de esta forma, podemos decir que esta cumple con las siguientes condiciones:

Esta función corresponde a valores desde el 0% de la población acumulada hasta el 100% de la población acumulada, es decir, $Dom(L) = [0,1]$ .
Esta función corresponde a valores desde el 0% de ingresos acumulados hasta el 100% de los ingresos acumulados, es decir, $Rgo(L) = [0,1]$ .
El 0% de los ingresos es repartido entre el 0% de la población, es decir, $L(0)=0$ .
El 100% de los ingresos es repartido entre el 110% de la población, es decir, $L(1)=1$ .
La distribución de los ingresos nunca es equitativa, es decir, $L(x) < x$ para todo $x$ en su dominio.

Este último punto se debe a que la distribución equitativa de los ingresos se representa con la función identidad, es decir, con la función $f(x)=x$ ; y es conocida como la Línea de Igualdad Perfecta. La Curva de Lorenz se representa gráficamente con una función estrictamente creciente por debajo de la recta identidad de la siguiente forma:

La Curva de Lorenz o Línea de Desigualdad Perfecta | totumat.com

Veamos en los siguientes ejemplos algunas Curva de Lorenz y la distribución de los ingresos que estas describen.

Ejemplos

Ejemplo 1

Considere la función $L(x) = \frac{1}{3}x^2 + \frac{2}{3}x$ , esta es una Curva de Lorenz y sobre ella podemos considerar lo siguiente:

Si evaluamos esta función en $0.2$ , tenemos que $L(0.2) = \frac{1}{3}(0.2)^2 + \frac{2}{3}(0.2) = 0.1466$ esto implica que el 20% de la población percibe el 14.66% de los ingresos.
Si evaluamos esta función en $0.4$ , tenemos que $L(0.4) = \frac{1}{3}(0.4)^2 + \frac{2}{3}(0.4) = 0.32$ esto implica que el 40% de la población percibe el 32% de los ingresos.
Si evaluamos esta función en $0.75$ , tenemos que $L(0.75) = \frac{1}{3}(0.75)^2 + \frac{2}{3}(0.75) = 0.6875$ esto implica que el 75% de la población percibe el 68.75% de los ingresos.

La función $L(x)$ se representa gráficamente de la siguiente forma:

Ejemplo 2

Considere la función $L(x) = \frac{7}{18}x^6 + \frac{11}{18}x^2$ , esta es una Curva de Lorenz y sobre ella podemos considerar lo siguiente:

Si evaluamos esta función en $0.15$ , tenemos que $f(0.15) = \frac{7}{18}(0.15)^6 + \frac{11}{18}(0.15)^2 = 0.013$ esto implica que el 15% de la población percibe el 1.3% de los ingresos.
Si evaluamos esta función en $0.5$ , tenemos que $f(0.5) = \frac{7}{18}(0.5)^6 + \frac{11}{18}(0.5)^2 = 0.1588$ esto implica que el 50% de la población percibe el 15.88% de los ingresos.
Si evaluamos esta función en $0.8$ , tenemos que $f(0.8) = \frac{1}{3}(0.8)^2 + \frac{2}{3}(0.8) = 0.4930$ esto implica que el 80% de la población percibe el 49.30% de los ingresos.

La función $L(x)$ se representa gráficamente de la siguiente forma:

El Coeficiente de Gini

Es notable que en algunos casos la Curva de Lorenz está más cercana a la recta identidad pero en otros, está más lejana, lo que pudiera indicar que tan desigual es la distribución de los ingresos. Observando esta situación, vale la pena preguntarse: ¿habrá una forma cuantificar esta diferencia? La respuesta es sí.

El Coeficiente de Gini mide la separación de la Curva de Lorenz respecto a la Línea de Igualdad Perfecta para determinar el grado de desigualdad que existe en la distribución de los ingreso, para llevar a cabo esta medición, consideramos las áreas A (roja) y B (azul) expresadas en el siguiente gráfico:

La Curva de Lorenz, áreas y Coeficiente de Gini | totumat.com

El área A es el área entre la Línea de Igualdad Perfecta y la Curva de Lorenz.
El área B es el área bajo la Curva de Lorenz.

El Coeficiente de Gini se determina calculando el cociente entre la área A y la suma de las áreas A+B, es decir,

$\frac{A}{A+B}$

Pero podemos notar inmediatamente que la suma de las áreas $A+B$ es justamente el área de un triángulo de base igual a $1$ y de altura igual a $1$ , por lo tanto, el área de este triángulo es $\frac{1}{2}$ . De esta forma, si efectuamos siguiente división

$\dfrac{ \ A \ }{\frac{1}{2}}$

Obtenemos una nueva expresión para calcular el Coeficiente de Gini, que será multiplicar el área A por 2:

$2 \cdot A$

Esta fórmula para calcular el Coeficiente de Gini nos indica que tan amplia es el área A y en consecuencia, qué tan alejada está la distribución de los ingresos de una distribución equitativa perfecta. Es por esto que al calcular este coeficiente, debemos tomar en cuenta que:

Si el Coeficiente de Gini está cercano a cero, esto quiere decir que la Curva de Lorenz está cerca de la Línea de Igualdad Perfecta y en consecuencia, la distribución de los ingresos tiende a ser equitativa.
Si el Coeficiente de Gini está cercano a uno, esto quiere decir que la Curva de Lorenz está alejada de la Línea de Igualdad Perfecta y en consecuencia, la distribución de los ingresos tiende a ser desigual.

En los siguientes ejemplos, veremos usaremos la fórmula para calcular el Coeficiente de Gini y veremos su interpretación.

Ejemplos

Ejemplo 3

Considerando la Curva de Lorenz $L(x) = \frac{1}{3}x^2 + \frac{2}{3}x$ , calcule el Coeficiente de Gini e interprete su resultado.

Representamos gráficamente la función $L(x)$ e identificamos las áreas involucradas para el cálculo del Coeficiente de Gini.

Calculamos el área A, identificada con rojo:

$A \ = \ \int_{0}^{1} \left( x - L(x) \right) \ dx$

$\ = \ \int_{0}^{1} \left( x - \left( \frac{1}{3}x^2 + \frac{2}{3}x \right) \right) \ dx$

$\ = \ \left. \left( \frac{x^2}{2} - \frac{1}{3} \frac{x^3}{3} - \frac{2}{3} \frac{x^2}{2} \right) \right|_{0}^{1}$

$\ = \ \left( \frac{(1)^2}{2} - \frac{1}{3} \frac{(1)^3}{3} - \frac{2}{3} \frac{(1)^2}{2} \right) - \left( \frac{(0)^2}{2} - \frac{1}{3} \frac{(0)^3}{3} - \frac{2}{3} \frac{(0)^2}{2} \right)$

$\ = \ 0.0555$

Por lo tanto, el Coeficiente de Gini es:

$2 \cdot A = 2 \cdot 0.0555 = 0.1111$

Al estar este valor cercano a cero, concluimos que la distribución de los ingresos tiende a ser equitativa.

Considerando la Curva de Lorenz $L(x) = \frac{7}{18}x^6 + \frac{11}{18}x^3$ , calcule el Coeficiente de Gini e interprete su resultado.

Representamos gráficamente la función $L(x)$ e identificamos las áreas involucradas para el cálculo del Coeficiente de Gini.

Calculamos el área A, identificada con rojo:

$A \ = \ \int_{0}^{1} \left( x - L(x) \right) \ dx$

$\ = \ \int_{0}^{1} \left( x - \left( \frac{7}{18}x^6 + \frac{11}{18}x^3 \right) \right) \ dx$

$\ = \ \left. \left( \frac{x^2}{2} - \frac{7}{18} \frac{x^7}{7} - \frac{11}{18} \frac{x^4}{4} \right) \right|_{0}^{1}$

$\ = \ \left( \frac{(1)^2}{2} - \frac{7}{18} \frac{(1)^7}{7} - \frac{11}{18} \frac{(1)^4}{4} \right) - \left( \frac{(0)^2}{2} - \frac{7}{18} \frac{(0)^7}{7} - \frac{11}{18} \frac{(0)^4}{4} \right)$

$\ = \ 0.2916$

Por lo tanto, el Coeficiente de Gini es:

$2 \cdot A = 2 \cdot 0.2916 = 0.5833$

Al estar este valor está más cercano a uno, que a cero, concluimos que la distribución de los ingresos tiende a ser desigual.

R: Estimadores Mínimos Cuadrados Ordinarios (MCO)

27.04.202107.12.2022 Anthonny Arias-García5 comentarios

El análisis de regresión sienta la base para los estudios econométricos y a su vez, estos se fundamentan formulando modelos lineales con dos variables: una independiente y otra dependiente; este tipo de modelos definen rectas, es decir, aquellos que se expresan de la siguiente forma:

$Y = \beta_1 + \beta_2 X$

También pudiera interesarte

Linealidad

Al mencionar la linealidad en una relación entre variables, siempre es importante especificar respecto a qué elemento de la relación, es dicha relación, lineal. Formalmente, diremos que una relación es lineal respecto a un elemento de la ecuación, si dicho elemento no está siendo multiplicada por sí mismo o si permanece inalterado por alguna función en la expresión, por ejemplo, la siguiente ecuación

$Y = \beta_1^2 + \beta_2 \cdot \ln(X)$

Es una ecuación lineal respecto respecto la variable $Y$ y el parámetro $\beta_2$ , debido a que estos dos elementos permanecen inalterados. Sin embargo, no es lineal respecto al parámetro $\beta_1$ pues este está multiplicado por sí mismo, tampoco es lineal respecto a la variable $X$ pues esta está alterada por la función logaritmo neperiano.

La linealidad respecto a los parámetros representa una base en la que se fundamentan los Modelos Lineales que estudiaremos. Es por esto que, usualmente, el término regresión lineal hace referencia a la linealidad de los parámetros. Por lo tanto, puede o no ser lineal en las variables.

El Modelo de Regresión Lineal

Todo estudio de índole estadístico está sometido a un error de aproximación y la econometría no escapa de esta característica, de forma que, al efectuar un censo poblacional, se puede estimar un modelo definido por la Función de Regresión Poblacional (FRP), expresado de la siguiente manera:

$Y_i = \beta_1 + \beta_2 X_i + u_i$

Sin embargo, llevar a cabo un censo puede resultar costoso en todos los aspectos, es por esto que se recurre a muestras poblacionales, a partir de las cuales se puede estimar un modelo definido por la Función de Regresión Muestral (FRM), expresado de la siguiente manera:

$\hat{Y}_i = \hat{\beta}_1 + \hat{\beta}_2 x_i + \hat{u}_i$

Y si bien el objetivo principal del análisis de regresión es estimar la FRP con base en la FRM, siempre se debe tomar en cuenta que: debido a fluctuaciones muestrales, la estimación de la FRP basada en la FRM es, en el mejor de los casos, una aproximación.

Mínimos Cuadrados Ordinarios (MCO)

Entonces, los valores de $\beta_1$ y $\beta_2$ se pueden estimar a partir de una muestra, usando un modelo que cuente con el término de error $\hat{u}_i$ más pequeño posible, sin embargo, no podemos permitir que estos errores se anulen.

El Método de los Mínimos Cuadrados Ordinarios (MCO) que consiste en considerar, de todos los modelos posibles, el modelo tal que la suma de los cuadrados de los residuos $\hat{u}_i$ sea la más pequeña, es decir, tal que la siguiente suma sea la más pequeña:

$\sum \hat{u}^2$

Llevando a cabo los cálculos necesarios para que esto se cumpla, se determina que los valores que estiman a $\beta_1$ y $\beta_2$ , es decir, los estimadores $\hat{\beta}_1$ y $\hat{\beta}_2$ se calculan de la siguiente forma:

El valor $\beta_2$ se conoce como la pendiente y su estimador es:

$\hat{\beta}_2 = \dfrac{\sum x_i y_i}{\sum x_i^2}$

El valor $\beta_1$ se conoce como el intercepto y su estimador es:

$\hat{\beta}_1 = \overline{Y} - \hat{\beta}_2 \overline{X}$

Conociendo estas dos expresiones, podemos hacer los cálculos correspondientes en R, pues calculando la media de las variables $X$ y $Y$ , usamos la siguiente sintaxis para calcular los estimadores

m.X <- mean(X)
m.Y <- mean(Y)
beta2 <- sum((X - m.X)*(Y - m.Y))/sum((X - m.X)^2)
beta1 <- m.Y - beta2*m.X

Ejemplo

Observación	Salario	Escolaridad
1	4.4567	6
2	5.77	7
3	5.9787	8
4	7.3317	9
5	7.3182	10
6	6.5844	11
7	7.8182	12
8	7.8351	13
9	11.0223	14
10	10.6738	15
11	10.8361	16
12	13.615	17
13	13.531	18

Tabla 3.2

Si queremos definir un modelo que describa el salario de una persona en función del nivel de estudio que esta persona tenga, empezamos por definir las variables salario y escolaridad, usando las siguientes instrucciones:

escolaridad <- c(6,7,8,9,10,11,12,13,14,15,16,17,18)
salario <- c(4.4567,5.77,5.9787,7.3317,7.3182,6.5844,7.8182,7.8351,11.0223,10.6738,10.8361,13.615,13.531)

Una vez definidas estas variables, podemos definir nuevas variables para almacenar la media de cada una de ellas:

m.escolaridad <- mean(escolaridad)
m.salario <- mean(salario)

Posteriormente, calculamos los estimadores:

beta2 <- sum( (escolaridad-m.escolaridad)*(salario-m.salario) )/sum( (escolaridad-m.escolaridad)^2 )
beta1 <- m.salario - beta2*m.escolaridad

Al ejecutar estas instrucciones definimos las variables y podemos ver los valores que cada una de ellas tienen, particularmente la de los estimadores que son las que nos interesan.

Modelo Lineal de Salario en función de Escolaridad | totumat.com

Mi recomendación es usar el símbolo de numeral «#» para hacer comentarios en el script y mantener orden en las instrucciones que escribimos o entender porqué las escribimos, les comparto como haría yo estas anotaciones.

Habiendo calculado los valores de los estimadores, concluimos que el modelo lineal determinado por el método de los Mínimos Cuadrados Ordinarios, que estima el comportamiento de los valores expuestos en la Tabla 3.2 es el siguiente:

$Salario = -0.0144 + 0.7240 \cdot Escolaridad$

Anuncios

La instrucción `lm`

También podemos recurrir a la instrucción lm para definir un modelo lineal, de forma que si queremos definir a la variable $Y$ en función de la variable $X$ , entonces usamos la siguiente sintaxis:

lm(Y ~ X)

Note que se ha usado la virguilla (~) para definir la relación entre las dos variables. Entonces, continuando con nuestro ejemplo, podemos definir el modelo lineal que describe el Salario en función de la Escolaridad usando la siguiente sintaxis:

lm(salario ~ escolaridad)

Al ejecutar esta instrucción, en la consola deberá aparecer lo siguiente:

> lm(salario ~ escolaridad)
Call:
lm(formula = salario ~ escolaridad)
Coefficients:
(Intercept)  escolaridad  
   -0.01445      0.72410

En su pantalla debería aparecer:

Excedente de los Consumidores y de los Productores – Caso no lineal

26.04.202107.09.2025 Anthonny Arias-García1 comentario

Al estudiar el mercado, es notorio que los productores siempre querrán vender a un precio elevado y los consumidores siempre querrán comprar a un precio bajo. El punto de equilibrio del mercado permite establecer un consenso entre las dos partes, sin embargo, ¿qué tanto beneficia este consenso a las partes?

También pudiera interesarte

Excedente de los Consumidores

Suponga que usted va al supermercado con el objetivo de comprar un producto y que cuando lo va a pagar, recibe la grata sorpresa de que está más barato de lo que usted pensaba, esta situación tiene una interpretación formal. Si observamos la función de demanda de un determinado artículo, podemos notar que si se fija el precio de cada unidad en $p_1$ Perolitos (Ps.), los consumidores estarán dispuestos a comprar $q_1$ unidades de dicho artículo.

Sin embargo, una vez que se ha fijado el punto de equilibrio $(q_0,p_0)$ , podemos notar que aquellos consumidores que están dispuestos a comprar $q_1$ unidades cuando el precio se había fijado en $p_1$ Ps., ahora comprarán las mismas $q_1$ unidades pagando cada unidad en un menor precio de $p_0$ Ps.

De esta forma, si un consumidor pensaba gastar $p_1 \cdot q_1$ Ps. (precio por unidad multiplicado por la cantidad adquirida), una vez que se ha fijado el precio de equilibrio, gastará $p_0 \cdot q_1$ Ps. Esto genera un beneficio para los consumidores, y a partir de este hecho surge la siguiente pregunta: ¿es posible cuantificar este beneficio?

Para responder a esta pregunta, supongamos que la cantidad de unidades que los consumidores piensan comprar no es fija sino que es una gama representada por un rango de unidades comprendidas entre ninguna unidad y la cantidad $q_0$ , fijada por el punto de equilibrio. El gasto que pagarían originalmente, está representado por el área que está debajo de la función de demanda de la siguiente forma,

Pero como al final los consumidores están pagando un precio de $p_0$ Ps. por cada unidad, el beneficio generado al fijar el equilibrio, está representado por el área que está debajo de la función de demanda y por encima del precio de equilibrio de la siguiente forma,

El área que representa el beneficio para los consumidores una vez que se ha fijado el precio de equilibrio se llama Excedente de los Consumidores o Superávit de los Consumidores, y lo podemos medir calculando el área que se encuentra entre la función de demanda, la recta que define del precio de equilibrio y el Eje P.

Por lo tanto, si la función de demanda está denotada de la forma $D(q)$ , determinamos el excedente de los consumidores calculando la siguiente integral definida:

$\displaystyle E.C. \ = \ \int_{0}^{q_0} \left( D(q) - p_0 \right) \ dq$

Nota: Perolitos (Ps.) es la moneda oficial de totumat.

Excedente de los Productores

Suponga que usted es productor de un artículo pero luego de estudiar los costos y un posible precio de venta para recibir unos ingresos aceptables, recibe la grata sorpresa de que puede fijar un precio por encima de lo que usted pensaba, esta situación tiene una interpretación formal. Si observamos la función de oferta de un determinado artículo, podemos notar que los productores estarán dispuestos a ofertar $q_1$ unidades de dicho artículo si se fija el precio de cada unidad en $p_1$ Perolitos (Ps.),

Sin embargo, una vez que se ha fijado el punto de equilibrio $(q_0,p_0)$ , podemos notar que aquellos productores que están dispuestos a ofertar $q_1$ unidades cuando el precio se había fijado en $p_1$ Ps., ahora ofertarán las mismas $q_1$ unidades vendiendo cada unidad en un mayor precio de $p_0$ Ps.

De esta forma, si un productor pensaba recibir $p_1 \cdot q_1$ Ps. (precio por unidad multiplicado por la cantidad ofertada), una vez que se ha fijado el precio de equilibrio, recibir $p_0 \cdot q_1$ Ps. Esto genera un beneficio para los productores, y a partir de este hecho surge la siguiente pregunta: ¿es posible cuantificar este beneficio?

Para responder a esta pregunta, supongamos que la cantidad de unidades que los productores piensan ofertar no es fija sino que es una gama representada por un rango de unidades comprendidas entre ninguna unidad y la cantidad $q_0$ , fijada por el punto de equilibrio. Los ingresos que recibirían originalmente, están representado por el área que está debajo de la función de oferta de la siguiente forma,

Pero como al final los productores están vendiendo a un precio de $p_0$ Ps. por cada unidad, el beneficio generado al fijar el equilibrio, está representado por el área que está debajo del precio de equilibrio y por encima de la función de oferta de la siguiente forma,

El área que representa el beneficio para los productores una vez que se ha fijado el precio de equilibrio se llama Excedente de los Productores o Superávit de los Productores, y lo podemos medir calculando el área del triángulo que genera la función de oferta, la función del precio de equilibrio y el Eje P.

Por lo tanto, si la función de oferta está denotada de la forma $O(q)$ , determinamos el excedente de los productores calculando la siguiente integral definida:

$\displaystyle E.P. \ = \ \int_{0}^{q_0} \big( p_0 - O(q) \big) \ dq$

Consideremos en los siguientes ejemplos cómo calcular el excedente de los consumidores y el excedente de los fabricantes considerando la curva de demanda y la curva de oferta del mercado.

Ejemplos

Ejemplo 1

Considerando la ecuación de demanda $p = -\frac{67}{100}q +126$ y la ecuación de oferta $p = \frac{13}{25}q^2 +36$ , calcule el punto de equilibrio del mercado; posteriormente calcule el excedente de los consumidores y el excedente de los fabricantes.

Para calcular el punto de equilibrio del mercado debemos igualar las expresiones que definen ambas rectas y luego planteamos una ecuación cuadrática para calcular $q$ .

$\displaystyle -\frac{67}{100}q +126 = \frac{13}{25}q^2+36$

$\displaystyle \Rightarrow \ -\frac{67}{100}q +126 - \frac{13}{25}q^2 - 36 = 0$

$\displaystyle \Rightarrow \ - \frac{13}{25}q^2 -\frac{67}{100}q + 90 = 0$

$\displaystyle \Rightarrow \ \frac{13}{25}q^2 + \frac{67}{100}q - 90 = 0$

Para calcular la solución de esta ecuación cuadrática utilizamos el método de discriminante:

$\displaystyle q \ = \ \dfrac{-b \pm \sqrt{b^2-4 \cdot a \cdot c}}{2 \cdot a}$

$\displaystyle \ = \ \dfrac{- \frac{67}{100} \pm \sqrt{\left( \frac{67}{100} \right)^2-4 \cdot \left( \frac{13}{25} \right) \cdot \left( - 90 \right)}}{2 \cdot \left( \frac{13}{25} \right)}$

De donde concluimos que $q \approx -13.84163$ ó $q \approx 12.50163$ , pero al ser $q$ una variable que representa cantidades, consideramos únicamente su valor positivo.

Una vez calculado el valor de $q$ , lo sustituimos en la función de nuestra preferencia y calculamos el valor de $p$ . Sustituyamos en este caso el valor de $q \approx 12.50163$ en la ecuación de demanda.

$\displaystyle p = \ -\frac{67}{100} \cdot \left( 12.50 \right) + 126 \ \approx \ 117.6239$

Por lo tanto, el punto de equilibrio del mercado $\left( 12.50163 ; 117.6239 \right)$ . Grafiquemos ahora el punto de equilibrio del mercado e identifiquemos las áreas que definen los excedentes.

Excedente de los Productores y de los Consumidores, ejemplo. | totumat.com

Calculamos el Excedente de los Consumidores:

$\displaystyle E.C. \ = \ \int_{0}^{q_0} \left( D(q) - p_0 \right) \ dq$

$\displaystyle \ = \ \int_{0}^{12.50} \left( -\frac{67}{100}q +126 - 117.62 \right) \ dq$

$\displaystyle \ = \ \int_{0}^{12.50} \left( -\frac{67}{100}q + 8.38 \right) \ dq$

$\displaystyle \ = \ \left. \left( -\frac{67}{100} \frac{q^2}{2} + 8.38q \right) \right|_{0}^{12.05}$

$\displaystyle \ = \ \left( -\frac{67}{100} \frac{(12.05)^2}{2} + 8.38(12.05) \right) - \left( -\frac{67}{100} \frac{(0)^2}{2} + 8.38(0) \right)$

$\displaystyle \ = \ 52.41$

Calculamos el Excedente de los Productores:

$\displaystyle E.P. \ = \ \int_{0}^{q_0} \left( p_0 - O(q) \right) \ dq$

$\displaystyle \ = \ \int_{0}^{12.05} \left( 117.62 - \frac{13}{25}q^2 - 36 \right) \ dq$

$\displaystyle \ = \ \int_{0}^{12.05} \left( 81.62 - \frac{13}{25}q^2 \right) \ dq$

$\displaystyle \ = \ \left. \left( 81.62q - \frac{13}{25} \frac{q^3}{3} \right) \right|_{0}^{12.05}$

$\displaystyle \ = \ \left( 81.62 (12.05) - \frac{13}{25} \frac{(12.05)^3}{3} \right) - \left( 81.62(0) - \frac{13}{25} \frac{(0)^3}{3} \right)$

$\ = \ 680.24$

Ejemplo 2

Considerando la ecuación de demanda $p = -\frac{1}{10}q^2 +115$ y la ecuación de oferta $p = \frac{87}{100}q +11$ , calcule el punto de equilibrio del mercado; posteriormente calcule el excedente de los consumidores y el excedente de los fabricantes.

Para calcular el punto de equilibrio del mercado debemos igualar las expresiones que definen ambas rectas y luego planteamos una ecuación cuadrática para calcular $q$ .

$\displaystyle -\frac{1}{10}q^2 +115 = \frac{87}{100}q +11$

$\displaystyle \Rightarrow \ -\frac{1}{10}q^2 +115 - \frac{87}{100}q - 11 = 0$

$\displaystyle \Rightarrow \ -\frac{1}{10}q^2 - \frac{87}{100}q + 104 = 0$

$\displaystyle \Rightarrow \ \frac{1}{10}q^2 + \frac{87}{100}q - 104 = 0$

Para calcular la solución de esta ecuación cuadrática utilizamos el método de discriminante:

$\displaystyle q \ = \ \dfrac{-b \pm \sqrt{b^2-4 \cdot a \cdot c}}{2 \cdot a}$

$\displaystyle \ = \ \dfrac{- \frac{87}{100} \pm \sqrt{\left( \frac{87}{100} \right)^2-4 \cdot \left( \frac{1}{10} \right) \cdot \left( - 104 \right)}}{2 \cdot \left( \frac{1}{10} \right)}$

De donde concluimos que $q \approx -33.41109$ ó $q \approx 31.67109$ , pero al ser $q$ una variable que representa cantidades, consideramos únicamente su valor positivo.

Una vez calculado el valor de $q$ , lo sustituimos en la función de nuestra preferencia y calculamos el valor de $p$ . Sustituyamos en este caso el valor de $q \approx 31.67$ en la ecuación de oferta.

$p = \ \frac{87}{100} (31.67) +11 \ \approx \ 38.55385$

Por lo tanto, el punto de equilibrio del mercado $\left( 31.67 ; 38.55 \right)$ . Grafiquemos ahora el punto de equilibrio del mercado e identifiquemos las áreas que definen los excedentes.

Calculamos el Excedente de los Consumidores:

$\displaystyle E.C. \ = \ \int_{0}^{q_0} \left( D(q) - p_0 \right) \ dq$

$\displaystyle \ = \ \int_{0}^{31.67} \left( -\frac{1}{10}q^2 +115 - 38.55 \right) \ dq$

$\displaystyle \ = \ \int_{0}^{31.67} \left( -\frac{1}{10}q^2 + 76.45 \right) \ dq$

$\displaystyle \ = \ \left. \left( -\frac{1}{10} \frac{q^3}{3} + 76.45q \right) \right|_{0}^{31.67}$

$\displaystyle \ = \ \left( -\frac{1}{10} \frac{(31.67)^3}{3} + 76.45(31.67) \right) - \left( -\frac{1}{10} \frac{(0)^3}{3} +76.45(0) \right)$

$\ = \ 1362.35$

Calculamos el Excedente de los Productores:

$\displaystyle E.P. \ = \ \int_{0}^{q_0} \left( p_0 - O(q) \right) \ dq$

$\displaystyle \ = \ \int_{0}^{31.67} \left( 38.55 - \frac{87}{100}q - 11 \right) \ dq$

$\displaystyle \ = \ \int_{0}^{31.67} \left( 27.55 - \frac{87}{100}q \right) \ dq$

$\displaystyle \ = \ \left. \left( 27.55 q - \frac{87}{100} \frac{q^2}{2} \right) \right|_{0}^{31.67}$

$\displaystyle \ = \ \left( 27.55 (31.67) - \frac{87}{100} \frac{(31.67)^2}{2} \right) - \left( 27.55 (0) - \frac{87}{100} \frac{(0)^2}{2} \right)$

$\ = \ 436.20$

totumat

¡Tu guía de matemáticas!

Autor: Anthonny Arias-García

R: Diagrama de Dispersión

Diagrama de Dispersión

Ejemplo

Ejemplo para los residuos

Verbos para redactar competencias

La Curva de Lorenz y el Coeficiente de Gini

La Curva de Lorenz

Ejemplos

Ejemplo 1

Ejemplo 2

El Coeficiente de Gini

Ejemplos

Ejemplo 3

R: Estimadores Mínimos Cuadrados Ordinarios (MCO)

Linealidad

El Modelo de Regresión Lineal

Mínimos Cuadrados Ordinarios (MCO)

Ejemplo

La instrucción `lm`

Excedente de los Consumidores y de los Productores – Caso no lineal

Excedente de los Consumidores

Excedente de los Productores

Ejemplos

Ejemplo 1

Ejemplo 2

Diagrama de Dispersión

Ejemplo

Ejemplo para los residuos

Comparte

Comparte

La Curva de Lorenz

Ejemplos

Ejemplo 1

Ejemplo 2

El Coeficiente de Gini

Ejemplos

Ejemplo 3

Comparte

Linealidad

El Modelo de Regresión Lineal

Mínimos Cuadrados Ordinarios (MCO)

Ejemplo

La instrucción lm

Comparte

Excedente de los Consumidores

Excedente de los Productores

Ejemplos

Ejemplo 1

Ejemplo 2

Comparte

La instrucción `lm`