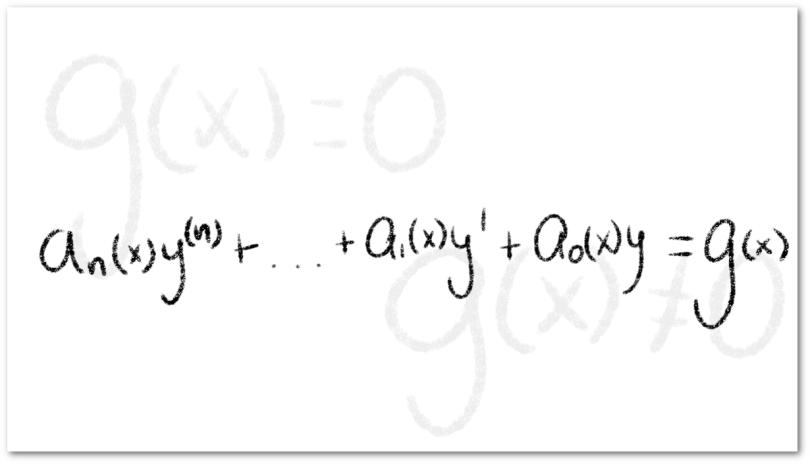Etiqueta: Ecuaciones Homogéneas

Ecuaciones Diferenciales Ordinarias Lineales Homogéneas y No-Homogéneas

Anthonny Arias-García3 comentarios
  1. Principio de Superposición para Ecuaciones Homogéneas
    1. Teorema (Principio de Superposición – Ecuaciones Homogéneas)
  2. Soluciones Linealmente Dependientes e Independientes

Al estudiar ecuaciones diferenciales ordinarias lineales de primer orden, aquellas expresadas de la forma a_1(x) y' + a_0(x) y = g(x), fue de vital importancia considerar el valor de la función g(x) pues nos permitió establecer una nueva forma de clasificar este tipo de ecuaciones diferenciales.

La situación no será diferente cuando estudiemos ecuaciones diferenciales ordinarias lineales de orden superior, pues al estar estas expresadas de la siguiente forma:

a_n(x) y^{(n)} + a_{n-1}(x) y^{(n-1)} + \ldots + a_1(x) y' + a_0(x) y = g(x)

Diremos que una ecuación diferencial ordinaria lineal es homogénea si g(x)=0, y por otra parte, diremos que es no-homogénea si g(x) \neq 0. En los siguientes ejemplos ilustraremos esta idea con mayor precisión.

También pudiera interesarte

Ejemplos

Ejemplo 1

La siguiente ecuación diferencial ordinaria lineal de segundo orden es homogénea, pues g(x)=0

2 y'' + 3y' +5y = 0

Ejemplo 2

La siguiente ecuación diferencial ordinaria lineal de tercer orden es homogénea, pues g(x)=0

-5 y''' + 7x^3y^4 = 0

Ejemplo 3

La siguiente ecuación diferencial ordinaria lineal de segundo orden es no-homogénea, pues g(x)=10x^3

3x^2 y'' + 7xy'+ 9 = 10x^3

Ejemplo 4

La siguiente ecuación diferencial ordinaria lineal de segundo orden es no-homogénea, pues g(x)=-7

\ln(x) y'' + 6\ln(x)y = -7

Ejemplo 5

La siguiente ecuación diferencial ordinaria lineal de tercer orden es no-homogénea, pues g(x)=\textit{\Large e}^x

\frac{11}{x}y''' - x^3 y'' + 6y' + 10y = \textit{\Large e}^x

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.

Principio de Superposición para Ecuaciones Homogéneas

Hemos mencionado antes que una ecuación diferencial ordinaria de orden superior puede tener varias soluciones si se presenta un problema de condiciones en la frontera.

El siguiente teorema nos permitirá sentar una base para el calculo de la solución de las ecuaciones diferenciales ordinarias lineales homogéneas tomando en cuenta las diferentes soluciones que esta puede tener.

Teorema (Principio de Superposición – Ecuaciones Homogéneas)

Si y_1,y_2, \ldots ,y_k son k soluciones de una ecuación diferencial ordinaria lineal homogénea de la forma

a_n(x) y^{(n)} + a_{n-1}(x) y^{(n-1)} + \ldots + a_1(x) y' + a_0(x) y = 0

definidas en un intervalo I y c_ 1, c_2, \ldots , c_k son constantes reales, entonces la combinación lineal

y = c_ 1y_1 + c_2 y_2 + \ldots + c_k y_k

también será una solución de la ecuación diferencial en el intervalo I.

De este teorema se derivan dos afirmaciones que nos serán de utilidad a la hora de definir la solución de una ecuación diferencial y es que podemos notar que al ser c_ 1, c_2, \ldots , c_k cualesquiera constantes reales, estas pudieran ser cero. Entonces, si y_p es una de las soluciones, tenemos que:

  • Cualquier múltiplo de la solución y_p, es decir, cualquier función de la forma c \cdot y_p es una solución de la ecuación.
  • Si todas las constantes son iguales a cero, entonces la función constante igual a cero, es decir, y=0 también es solución de la ecuación. Esta solución se conoce como la solución trivial.

Soluciones Linealmente Dependientes e Independientes

Diremos que un conjunto de k soluciones y_1,y_2, \ldots ,y_k definidas en un intervalo I, es linealmente dependiente si cualquiera de estas soluciones se puede expresar como una combinación lineal de las demás soluciones, es decir, tal que existen constantes c_ 1, c_2, \ldots , c_k con al menos una de ellas diferente de cero, tal que

c_ 1y_1 + c_2 y_2 + \ldots + c_k y_k = 0

Por otra parte, diremos que un conjunto de k soluciones y_1,y_2, \ldots ,y_k definidas en un intervalo I, es linealmente independiente si no son linealmente dependientes, y más aún, si y_1,y_2, \ldots ,y_n es un conjunto de soluciones linealmente independiente de una ecuación diferencial ordinaria lineal homogénea de orden n, diremos que este es un conjunto fundamental de soluciones.

Si consideramos una ecuación diferencial ordinaria lineal homogénea de orden n cuyos coeficientes a_0(x), a_1(x) \ldots , a_n(x) son funciones continuas en un intervalo I, es decir, expresada de la siguiente manera

a_n(x) y^{(n)} + \ldots + a_1(x) y' + a_0(x) y = 0

Entonces siempre podemos garantizar que existe un conjunto fundamental de soluciones, e incluso, la solución general de esta ecuación se expresa como una combinación lineal de este conjunto de soluciones, es decir,

y = c_ 1y_1 + c_2 y_2 + \ldots + c_n y_n

Ecuaciones Homogéneas de grado alpha ⍺

Anthonny Arias-García1 comentario

Funciones Homogéneas de grado alpha ⍺

Las ecuaciones diferenciales que veremos a continuación se pueden reescribir como ecuaciones diferenciales de variables separables luego de recurrir a una variable auxiliar, sin embargo, debemos verificar primero que cumplan con una condición. Definamos entonces los elementos que determinarán el criterio para poder calcular su solución.

También pudiera interesarte

Decimos que una función f(x,y) es una función homogénea de grado \alpha si para algún número real \alpha se satisface las siguiente igualdad:

f(t \cdot x,t \cdot y)=t^{\alpha} \cdot f(x,y)

Veamos algunos ejemplos de este tipo de funciones para entender esta idea.

Ejemplos

Ejemplo 1

Verifique si la función que se presenta a continuación es una función homogénea de grado \alpha:

f(x,y) = x^2 - y^2

Para esto, evaluamos la función f en el punto (tx,ty) y manipulamos algebraicamente con el fin de sacar la forma t^{\alpha} como un factor común.

f(tx,ty)

\; = \; (tx)^2 - (ty)^2
\; = \; t^2x^2 - t^2y^2
\; = \; t^2(x^2 - y^2)
\; = \; t^2 f(x,y)

En este caso, decimos que la función f es una función homogénea de grado 2.

Ejemplo 2

Verifique si la función que se presenta a continuación es una función homogénea de grado \alpha:

f(x,y) = x^2 + xy

Para esto, evaluamos la función f en el punto (tx,ty) y manipulamos algebraicamente con el fin de sacar la forma t^{\alpha} como un factor común.

f(tx,ty)

\; = \; (tx)^2 + (tx)(ty)
\; = \; t^2x^2 + t^2xy
\; = \; t^2(x^2 + xy)
\; = \; t^2 f(x,y)

En este caso, decimos que la función f es una función homogénea de grado 2.

Ejemplo 3

Verifique si la función que se presenta a continuación es una función homogénea de grado \alpha:

f(x,y) = 4 x^2y^5 - 9x^4y^3

Para esto, evaluamos la función f en el punto (tx,ty) y manipulamos algebraicamente con el fin de sacar la forma t^{\alpha} como un factor común.

f(tx,ty)

\; = \; 4 (tx)^2(ty)^5 - 9(tx)^4(ty)^3
\; = \; 4(t^2x^2)(t^5y^5) - 9(t^4x^4)(t^3y^3)
\; = \; 4t^7x^2y^5 - 9t^7x^4y^3
\; = \; t^7(4x^2y^5 - 9x^4y^3)
\; = \; t^7 f(x,y)

En este caso, decimos que la función f es una función homogénea de grado 7.

Ejemplo 4

Verifique si la función que se presenta a continuación es una función homogénea de grado \alpha:

f(x,y) = 6 xy^3 + 5x^4 + 17

Para esto, evaluamos la función f en el punto (tx,ty) y manipulamos algebraicamente con el fin de sacar la forma t^{\alpha} como un factor común.

f(tx,ty)

\; = \; 6 (tx)(ty)^3 + 5(tx)^4 + 17
\; = \; 6 (tx)(t^3y^3) + 5(t^4x^4) + 17
\; = \; 6 t^4xy^3 + 5 t^4x^4 + 17

En este caso, no es posible sacar t^4 como un factor común y en consecuencia, la función f no se puede expresar de la forma t^{\alpha} f(x,y), por lo tango, no es una función homogénea de grado \alpha.

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.

Ecuaciones Homogéneas de grado alpha ⍺

Al considerar la ecuación diferencial M(x, y) dx + N(x, y) dy = 0, hemos podido clasificar algunas ecuaciones de esta forma como Ecuaciones Exactas y aunque hemos encontrado otras no exactas, se han podido reducir a ecuaciones exactas, sin embargo, no siempre podemos aplicar ese método establecido en estos casos.

Entonces, debemos establecer una nueva forma de clasificar este tipo de ecuaciones. Formalmente, si consideramos una ecuación diferencial expresada de la siguiente forma:

M(x, y) dx + N(x, y) dy = 0

Decimos que esta es una ecuación homogénea de grado \alpha si las funciones M(x,y) y N(x,y) son funciones de homogéneas de grado \alpha.

Si M(x, y) dx + N(x, y) dy = 0 es una ecuación diferencial ordinaria homogénea de grado \alpha, será posible reducir esta ecuación a una ecuación diferencial homogénea de variables separables recurriendo a una de las siguientes variables auxiliares para efectuar una sustitución de variable

u=\frac{y}{x} \ \text{ o } \ v=\frac{x}{y}

Notando que podemos reescribir estas dos expresiones respectivamente de la siguiente forma:

y = ux \ \text{ o } \ x = vy

Veamos entonces con algunos ejemplos calcular la solución de este tipo de ecuaciones diferenciales.

Ejemplos

Ejemplo 5

Calcule la solución de la siguiente ecuación diferencial ordinaria

(x^2-2y^2)dx + (2x^2+3xy)dy = 0

Debemos recurrir a una sustitución de variable para reducirla a una ecuación diferencial de variables separables, pero antes es necesario verificar que las funciones M(x,y) = (x^2-2y^2) y N(x,y) = (2x^2+3xy) son ambas funciones homogéneas de grado \alpha.

M(tx,ty)

\; = \; (tx)^2-2(ty)^2
\; = \; t^2x^2-2t^2y^2
\; = \; t^2(x^2-2y^2)
\; = \; t^2 M(x,y)

N(tx,ty)

\; = \; 2(tx)^2+3(tx)(ty)
\; = \; 2t^2x^2+3t^2xy
\; = \; t^2(2x^2+3xy)
\; = \; t^2 N(x,y)

Habiendo verificado que M(x,y) y N(x,y) son ambas funciones homogéneas de grado 2, podemos recurrir a la siguiente variable auxiliar

u=\frac{y}{x} \Rightarrow y=ux

De esta forma, podemos sustituirla en nuestra ecuación diferencial. Notemos también, que si queremos hacer esta sustitución, debemos calcular el diferencial dy

dy = udx + xdu

Entonces, sustituimos los elementos y y dy en la ecuación diferencial.

(x^2-2y^2)dx + (2x^2+3xy)dy = 0

\Rightarrow \big( x^2-2(ux)^2 \big)dx + \big( 2x^2+3x(ux) \big)( udx + xdu) = 0

Una vez que hemos hecho la sustitución de las variables, manipulamos algebraicamente las expresiones que definen la ecuación diferencial con el fin de separar las variables.

( x^2-2u^2x^2 )dx + ( 2x^2+3x^2u)( udx + xdu) = 0

\; \Rightarrow \; ( x^2-2u^2x^2 )dx + ( 2x^2+3x^2u )udx + \big( 2x^2+3x^2u \big)xdu = 0

\; \Rightarrow \; ( x^2-2u^2x^2 )dx + ( 2x^2u+3x^2u^2 )dx + ( 2x^3+3x^3u )du = 0

\; \Rightarrow \; ( x^2-2u^2x^2 + 2x^2u+3x^2u^2 )dx + (2+3u ) x^3 du = 0

\; \Rightarrow \; ( 1 -2u^2 + 2u + 3u^2 ) x^2 dx + (2+3u ) x^3 du = 0

\; \Rightarrow \; ( 1 + 2u + u^2 ) x^2 dx + (2+3u ) x^3 du = 0

\; \Rightarrow \; ( 1 + 2u + u^2 ) x^2 dx = - (2+3u ) x^3 du

\; \Rightarrow \; \frac{x^2}{x^3}dx = -\frac{(2+3u )}{( 1 + 2u + u^2 )} du

\; \Rightarrow \; \frac{1}{x}dx = -\frac{(2+3u )}{( 1 + u )^2} du

Ya que las variables están separadas, procedemos a calcular las respectivas integrales notando que la integral del lado derecho, es decir, -\frac{(2+3u )}{( 1 + u )^2}; debe calcularse usando el método de las fracciones simples. Entonces,

\int -\frac{(2+3u )}{( 1 + u )^2} du = \int \frac{1}{x}dx

\; \Rightarrow \; -\frac{1}{1+u} - 3\ln(1+u) = ln(x) + c

\; \Rightarrow \; \frac{1}{1+u} + 3\ln(1+u) + ln(x) = c

Finalmente, sustituimos la variable u y obtenemos la solución general de la ecuación diferencial que viene expresada de forma implícita como

\frac{1}{1+\frac{y}{x}} + 3\ln \left(1+\frac{y}{x} \right) + \ln(x) = c