Hemos visto que el coeficiente de determinación nos permite determinar en qué medida dos variables están relacionadas, pero siempre resulta de interés preguntarse si es posible determinar la forma en que estas dos variables están relacionadas, particularmente, en qué medida están correlacionadas.
También pudiera interesarte
Coeficiente de Correlación Muestral
Considerando una de las fórmulas para calcular el coeficiente de determinación , definimos un nuevo valor que está íntimamente relacionado con dicha fórmula pero que conceptualmente son diferentes. Entonces, partiendo del hecho que,
Definimos un nuevo valor , conocido como el Coeficiente de Correlación Muestral, que mide el grado de asociación lineal entre dos variables y se calcula de la siguiente forma:
Podemos calcularlo en R usando la siguiente sintaxis:
r <- sum((X-m.X)*(Y-m.Y))/sqrt(sum((X - m.X)^2)*sum((Y - m.Y)^2))Es importante destacar que:
Aunque el coeficiente de correlación r es una medida de asociación lineal entre dos variables, este no implica necesariamente alguna relación causa-efecto.
Una ventaja en el cálculo de este coeficiente, es que es simétrico por la forma en que está definido, es decir, el coeficiente de correlación entre y
(
) es el mismo que entre
y
(
).
Interpretación Gráfica del Coeficiente de Correlación Muestral
A diferencia de , que está acotado por 0 y 1; el coeficiente de correlación muestral está acotado por -1 y 1, esto quiere decir que puede tomar valores negativos. Entonces, considerando que gráficamente es independiente del origen y de la escala, podemos considerar varias observaciones sobre este valor:
Si valor del coeficiente de correlación es exactamente igual a 1 (uno positivo), los datos están representados gráficamente sobre una línea recta creciente.

Si valor del coeficiente de correlación es exactamente igual a -1 (uno negativo), los datos están representados gráficamente sobre una línea recta decreciente.

Si valor del coeficiente de correlación está cercano a 1 (uno positivo), los datos representados gráficamente, tienen una clara tendencia lineal creciente pero no están exactamente alineados.

Si valor del coeficiente de correlación está cercano a -1 (uno negativo), los datos representados gráficamente, tienen una clara tendencia lineal decreciente pero no están exactamente alineados.

Si valor del coeficiente de correlación está cercano a 0 pero es positivo, los datos representados gráficamente, tienen una tendencia lineal creciente pero presentan una dispersión mayor a media que el valor de
está más cercano a cero.

Si valor del coeficiente de correlación está cercano a 0 pero es negativo, los datos representados gráficamente, tienen una tendencia lineal decreciente pero presentan una dispersión mayor a media que el valor de
está más cercano a cero.

Si la variable y la variable
son estadísticamente independientes, entonces valor del coeficiente de correlación
es igual a cero y en este caso, los datos representados gráficamente, no presentan ningún tipo de tendencia lineal.

Precaución: El coeficiente de correlación es una medida de asociación lineal (o dependencia lineal) solamente; su uso en la descripción de relaciones no lineales no tiene significado. Dicho esto, puede ocurrir que
sea igual a cero pero el conjunto de datos presente otro tipo de relación.

Ejemplo
Consideremos un pequeño conjunto de datos, particularmente, los datos que se encuentran en la Tabla 3.2 del libro de Econometría de Damodar N. Gujarati and Dawn Porter en su quinta edición. Este conjunto de datos proporciona los datos primarios que se necesitan para estimar el efecto cuantitativo de la escolaridad en los salarios:
| Observación | Salario | Escolaridad |
| 1 | 4.4567 | 6 |
| 2 | 5.77 | 7 |
| 3 | 5.9787 | 8 |
| 4 | 7.3317 | 9 |
| 5 | 7.3182 | 10 |
| 6 | 6.5844 | 11 |
| 7 | 7.8182 | 12 |
| 8 | 7.8351 | 13 |
| 9 | 11.0223 | 14 |
| 10 | 10.6738 | 15 |
| 11 | 10.8361 | 16 |
| 12 | 13.615 | 17 |
| 13 | 13.531 | 18 |
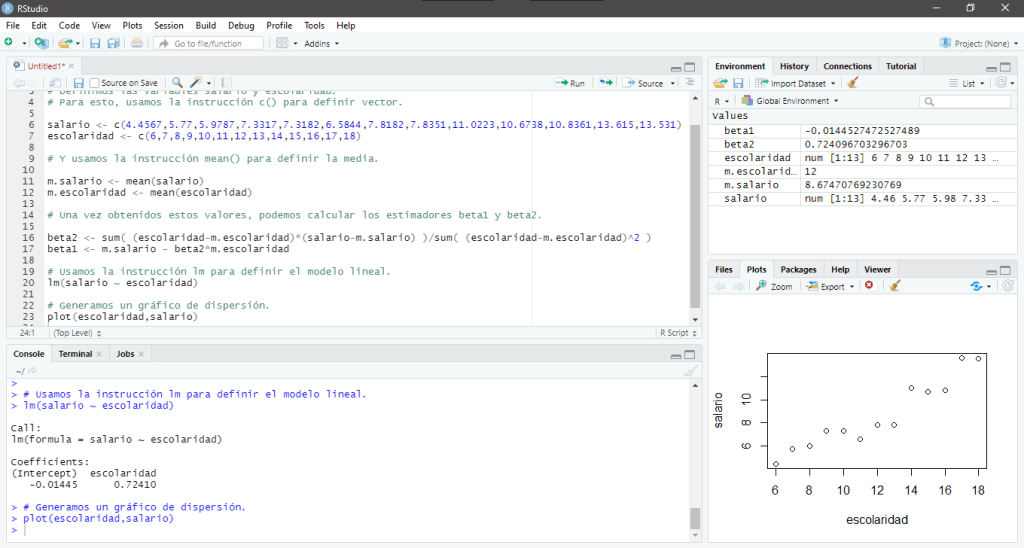
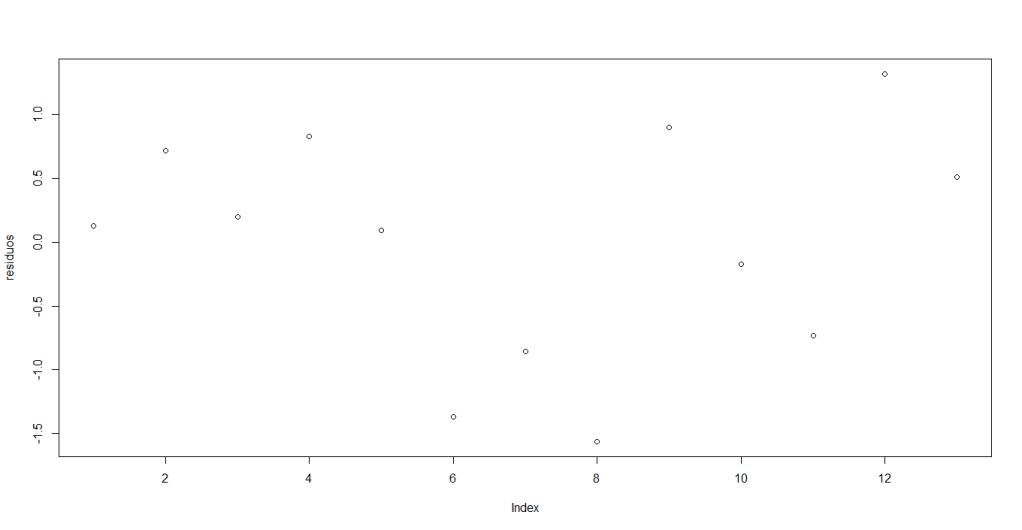
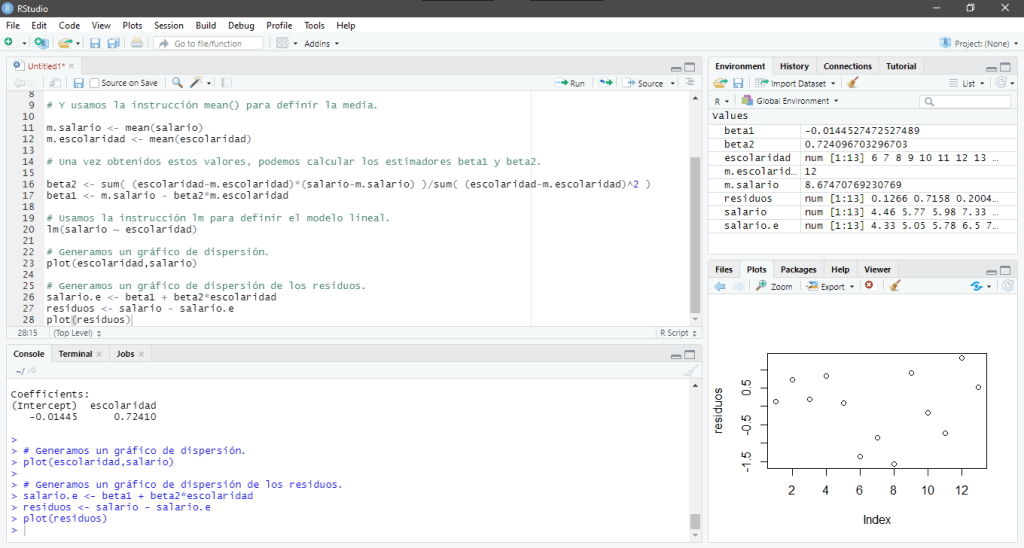
Una vez que hemos calculado el modelo lineal que define este conjunto de datos, podemos calcular el coeficiente de determinación para ver qué tan relacionadas están las variables Salario y Escolaridad, para esto, usamos la siguiente sintaxis:
r <- sum((escolaridad-m.escolaridad)*(salario-m.salario))/sqrt(sum((escolaridad - m.escolaridad)^2)*sum((salario - m.salario)^2))Al ejecutar estas instrucciones obtenemos coeficiente de correlación , que en este caso es igual a 0.9527809.
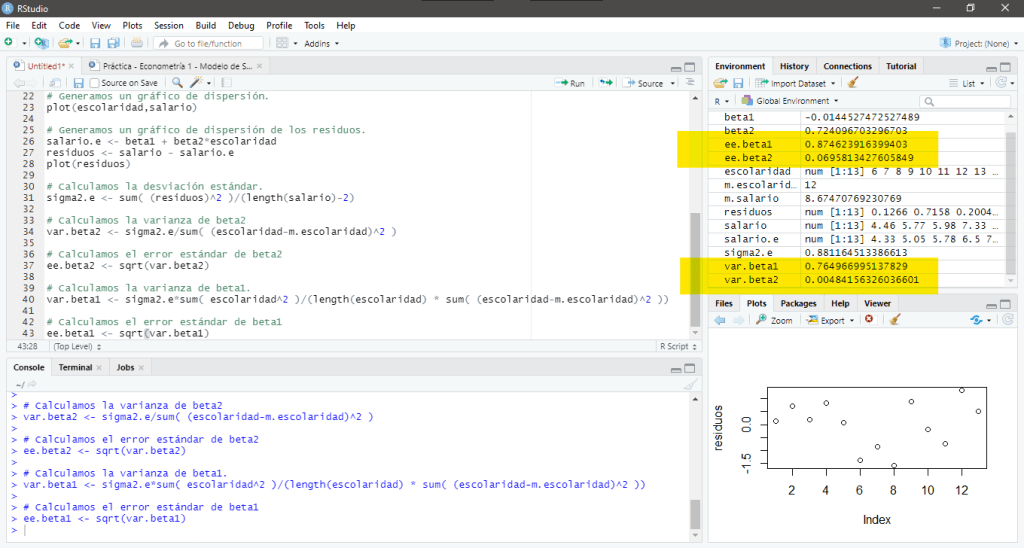
En su pantalla debería aparecer:

En este caso, el valor del coeficiente de correlación sugiere que la variable y la variable
definen un tendencia lineal creciente y es lo que se puede observar en el gráfico de dispersión.








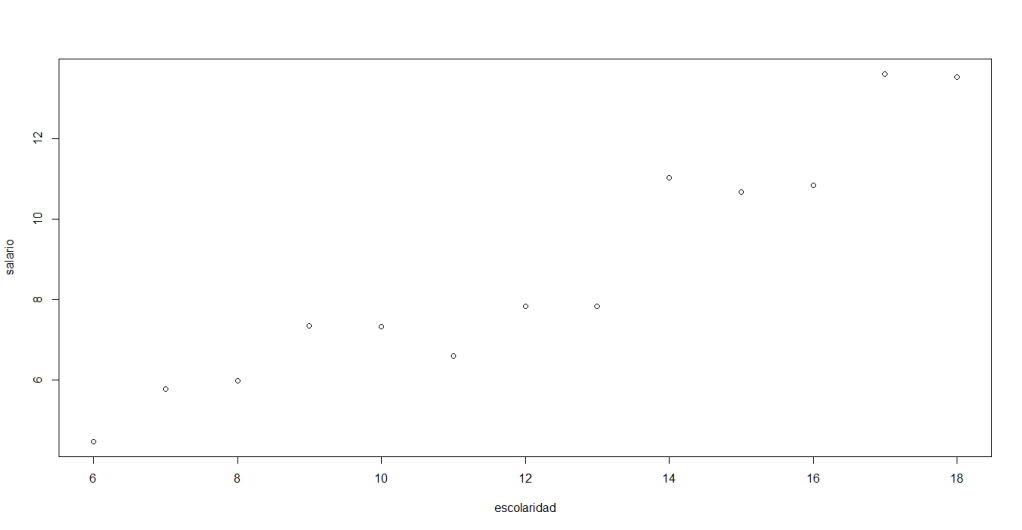

Debe estar conectado para enviar un comentario.