Autor: Anthonny Arias-García

Sub-Coordinador de Matemáticas de la Facultad de Ciencias Económicas y Sociales, Universidad de Los Andes, Mérida, Venezuela.
Ejercicios Propuestos

Ejercicios Propuestos – Propiedades de los Radicales

Anthonny Arias-GarcíaDeja un comentario

Factorice las siguientes expresiones descomponiendo cada uno de los elementos involucrados en factores primos y posteriormente usando las propiedades de los radicales.

  1. \sqrt[4]{76}
  2. \sqrt[6]{115}
  3. \sqrt[8]{49}
  4. \sqrt[10]{90}
  1. \sqrt{15^2} \cdot \sqrt[3]{25^5}
  2. \sqrt[3]{16^3} \cdot \sqrt[4]{14^4}
  3. \sqrt[4]{18^4} \cdot \sqrt[5]{20^3}
  4. \sqrt[5]{22^5} \cdot \sqrt[6]{44^2}
  1. \sqrt[3]{27 \cdot 30}
  2. \sqrt[5]{24 \cdot 16}
  3. \sqrt[7]{62 \cdot 20}
  4. \sqrt[9]{63 \cdot 98}
  1. \dfrac{\sqrt[4]{76}}{\sqrt[6]{115}}
  2. \dfrac{\sqrt[8]{49}}{\sqrt[10]{90}}
  3. \dfrac{\sqrt[12]{89}}{\sqrt[14]{30}}
  4. \dfrac{\sqrt[16]{65}}{\sqrt[18]{27}}

  1. \dfrac{\sqrt{15^2} \cdot \sqrt[3]{25^9}}{\sqrt[3]{16^3} \cdot \sqrt[4]{14^4}}
  2. \dfrac{\sqrt[5]{18^4} \cdot \sqrt[6]{20^7}}{\sqrt[8]{22^5} \cdot \sqrt[6]{44^3}}
  3. \dfrac{\sqrt[7]{28^6} \cdot \sqrt[8]{66^5}}{\sqrt[13]{87^8} \cdot \sqrt[8]{50^2}}
  4. \dfrac{\sqrt[9]{55^8} \cdot \sqrt[10]{61^3}}{\sqrt[18]{78^{11}} \cdot \sqrt[10]{72}}

  1. \dfrac{\sqrt[3]{27 \cdot 30}}{\sqrt[5]{24 \cdot 16}}
  2. \dfrac{\sqrt[7]{62 \cdot 20}}{\sqrt[9]{63 \cdot 98}}
  3. \dfrac{\sqrt[11]{81 \cdot 20}}{\sqrt[13]{46 \cdot 53}}
  4. \dfrac{\sqrt[15]{98 \cdot 54}}{\sqrt[17]{45 \cdot 75}}

Ejercicios Propuestos

Ejercicios Propuestos – Propiedades de las Potencias

Anthonny Arias-GarcíaDeja un comentario

Factorice y simplifique las siguientes expresiones descomponiendo cada uno de los elementos involucrados en factores primos y posteriormente usando las propiedades de las potencias.

  1. 78
  2. 72
  3. 45
  4. 52
  1. 28 \cdot 30
  2. 24 \cdot 14
  3. 60 \cdot 20
  4. 63 \cdot 96
  1. 15^2 \cdot 25^5
  2. 16^3 \cdot 14^4
  3. 18^4 \cdot 20^3
  4. 22^5 \cdot 44^2
  1. (17 \cdot 25)^5
  2. (16 \cdot 20)^4
  3. (52 \cdot 21)^3
  4. (22 \cdot 55)^2
  1. (17^{-1} \cdot 25^{14})^5
  2. (16^{-3} \cdot 20^{15})^4
  3. (52^{-5} \cdot 41^{23})^3
  4. (22^{-7} \cdot 85^{12})^2
  1. \dfrac{18}{3}
  2. \dfrac{24}{8}
  3. \dfrac{16}{6}
  4. \dfrac{42}{14}
  1. \dfrac{18^{10}}{3^5}
  2. \dfrac{24^9}{8^6}
  3. \dfrac{16^8}{6^7}
  4. \dfrac{42^7}{14^8}
  1. \dfrac{12^{-4}}{3^5}
  2. \dfrac{24^{-3}}{8^6}
  3. \dfrac{32^{-2}}{6^7}
  4. \dfrac{48^{-1}}{14^8}
  1. \dfrac{28 \cdot 30}{24 \cdot 14}
  2. \dfrac{60 \cdot 20}{63 \cdot 96}
  3. \dfrac{91 \cdot 84}{46 \cdot 50}
  4. \dfrac{42 \cdot 10}{62 \cdot 80}
  1. \dfrac{(17 \cdot 25)^5}{(16 \cdot 20)^4}
  2. \dfrac{(52 \cdot 21)^3}{(22 \cdot 55)^2}
  3. \dfrac{(64 \cdot 53)^5}{(14 \cdot 20)^4}
  4. \dfrac{(35 \cdot 32)^3}{(49 \cdot 45)^2}
  1. \dfrac{(17^{-1} \cdot 25^{14})^5}{(16^{-3} \cdot 20^{15})^4}
  2. \dfrac{(52^{-5} \cdot 41^{23})^3}{(22^{-7} \cdot 85^{12})^2}
  3. \dfrac{(63^{-1} \cdot 95^{14})^5}{(94^{-3} \cdot 93^{15})^4}
  4. \dfrac{(27^{-5} \cdot 66^{23})^3}{(16^{-7} \cdot 95^{12})^2}

Ejercicios Propuestos

Ejercicios Propuestos – Operaciones básicas entre números reales

Anthonny Arias-GarcíaDeja un comentario

Calcule el resultado de las siguientes expresiones matemáticas tomando en cuenta la jerarquía de las operaciones básicas y los signos de agrupación.

  1. 90 + 58 \cdot 13
  2. -54 + 3 \cdot 48
  3. 8 - 10 \cdot 12
  4. -25 - 78 \cdot 34

  1. ( 11 + 52) \cdot 13
  2. ( -72 + 19) \cdot 88
  3. ( 56 - 65) \cdot 39
  4. ( -51 - 33) \cdot 4

  1. 78 + ( 50 + 54) \cdot 72
  2. 5 + ( 73 - 84) \cdot 37
  3. 95 - ( 64 + 53) \cdot 39
  4. 87 - ( 64 - 27) \cdot 30

  1. 4^2 + ( 2 + 7) \cdot 4
  2. 2^3 + ( 6 - 3) \cdot 7
  3. 5^2 - ( 9 + 2) \cdot 4
  4. 4^3 - ( 9 - 10) \cdot 9

  1. 53 + [ 9^3 + ( 4 + 8) \cdot 2 ]
  2. 62 - [ 4^2 + ( 9 + 6) \cdot 6 ]
  3. 95 + [ 3^2 - ( 1 + 7) \cdot 6 ]
  4. 86 - [ 2^2 + ( 2 - 9) \cdot 9 ]

  1. 7 \cdot [ 4^3 + ( 7 + 1) \cdot 2 ] + 17
  2. 8 \cdot [ 2^2 - ( 1 + 3) \cdot 5 ] - 25
  3. 2 \cdot [ 4^2 - ( 3 - 8) \cdot 3 ] + 93
  4. 8 \cdot [ 4^2 - ( 1 - 2) \cdot 7 ] - 15

  1. (7^2 + 56 ) \cdot {6 + [ 6^2 + ( 5 + 6) \cdot 7 ] + 24}
  2. (2^2 - 69 ) \cdot {2 + [ 3^2 + ( 7 + 6) \cdot 7 ] - 71}
  3. (8^2 + 55 ) \cdot {8 - [ 10^2 + ( 9 - 9) \cdot 5 ] + 58}
  4. (2^2 - 99 ) \cdot {10 + [ 10^2 - ( 2 - 3) \cdot 1 ] + 81}

  1. \dfrac{ 68 + 96 \cdot 61 }{ 49 + 13 \cdot 78 }
  2. \dfrac{ 98 + 10 \cdot 28 }{ 11 - 82 \cdot 73 }
  3. \dfrac{ 53 - 93 \cdot 64 }{ 93 + 88 \cdot 92 }
  4. \dfrac{ 71 - 7 \cdot 77 }{ 43 - 62 \cdot 79 }

  1. 73 + 84 \cdot \dfrac{ 42 }{ 78 + 29 \cdot 69 }
  2. 8 + 85 \cdot \dfrac{ 1 }{ 11 - 39 \cdot 59 }
  3. 70 - 44 \cdot \dfrac{ 2 }{ 19 + 96 \cdot 38 }
  4. 35 - 86 \cdot \dfrac{ 62 }{ 68 - 40 \cdot 64 }

  1. \dfrac{ 32 + [ 8^2 + ( 10 + 1) \cdot 6 ] }{ 19 + [ 4^3 + ( 4 + 4) \cdot 5 ] }
  2. \dfrac{ 62 - [ 8^3 + ( 5 + 9) \cdot 2 ] }{ 54 - [ 10^3 - ( 2 + 4) \cdot 7 ] }
  3. \dfrac{ 76 - [ 5^2 - ( 4 + 7) \cdot 10 ] }{ 11 + [ 7^2 + ( 7 - 9) \cdot 2 ] }
  4. \dfrac{ 44 - [ 10^2 - ( 1 - 4) \cdot 8 ] }{ 49 - [ 5^3 - ( 1 - 1) \cdot 7 ] }

  1. 81 + 8^2 + \dfrac{ ( 1 - 8) \cdot 8 ] }{ 6 - [ 8^2 - ( 6 + 4) \cdot 8 ] }
  2. 89 + 7^3 + \dfrac{ ( 4 - 3) \cdot 8 ] }{ 88 - [ 8^3 - ( 7 + 3) \cdot 1 ] }
  3. 54 + 10^3 + \dfrac{ ( 3 - 4) \cdot 5 ] }{ 93 - [ 4^3 - ( 4 + 9) \cdot 9 ] }
  4. 52 + 4^3 + \dfrac{ ( 3 - 7) \cdot 10 ] }{ 70 - [ 5^2 - ( 7 + 8) \cdot 9 ] }

  1. \dfrac{ (4^3 - 68 ) \cdot {7 + [ 5^3 - ( 1 - 9) \cdot 6 ] + 52} }{ (2^3 - 91 ) \cdot {4 + [ 3^3 - ( 5 - 5) \cdot 10 ] + 19} }
  2. \dfrac{ (10^2 - 37 ) \cdot {10 + [ 9^2 - ( 10 - 4) \cdot 5 ] + 89} }{ (4^2 - 37 ) \cdot {10 + [ 9^3 - ( 4 - 10) \cdot 8 ] + 49} }
  3. \dfrac{ (7^3 - 38 ) \cdot {1 + [ 6^3 - ( 3 - 6) \cdot 6 ] + 93} }{ (9^3 - 61 ) \cdot {1 + [ 6^2 - ( 4 - 8) \cdot 2 ] + 17} }
  4. \dfrac{ (2^2 - 39 ) \cdot {1 + [ 3^2 - ( 3 - 1) \cdot 4 ] + 38} }{ (4^3 - 44 ) \cdot {10 + [ 6^3 - ( 10 - 2) \cdot 10 ] + 79} }

  1. (5^3 + 98 ) + \dfrac{ 3\cdot{5 + [ 9^2 + ( 2 + 10) \cdot 9 ] + 20} }{ (9^3 + 48 ) \cdot {2 + [ 6^3 + ( 1 + 4) \cdot 10 ] + 95} }
  2. (3^2 + 42 ) - \dfrac{ 7\cdot{3 + [ 2^3 + ( 1 + 7) \cdot 3 ] + 90} }{ (8^3 + 32 ) \cdot {8 + [ 3^2 + ( 1 + 10) \cdot 9 ] + 82} }
  3. -(2^2 + 5 ) + \dfrac{ 4\cdot{8 + [ 4^3 + ( 6 + 10) \cdot 7 ] + 21} }{ (8^2 + 81 ) \cdot {7 + [ 2^3 + ( 4 + 3) \cdot 2 ] + 26} }
  4. -(6^3 + 63 ) - \dfrac{ 6\cdot{5 + [ 8^2 + ( 5 + 2) \cdot 6 ] + 37} }{ (10^2 + 5 ) \cdot {1 + [ 6^2 + ( 3 + 1) \cdot 7 ] + 51} }

R: La instrucción lm()

Anthonny Arias-García2 comentarios

Introducir a la econometría requiere estudiar de forma minuciosa cada uno de los elementos que permiten el análisis de regresión y si bien podemos calcular cada uno de estos usando las fórmulas que provee la teoría, la idea de usar programas de paquetes estadísticos como R es usar instrucciones que nos permitan hacer este tipo de cálculos de forma automática.

También pudiera interesarte

La instrucción lm()

Si se cuentan con al menos dos variables, digamos Y y X, podemos determinar la Recta de Regresión Muestral usando la instrucción lm() usando la virgulilla ~ para definir la relación entre las dos variables. La sintaxis para definir un modelo lineal que describa a la variable dependiente Y en función de la variable independiente X es la siguiente:

lm(Y ~ x)

Al ejecutar esta instrucción se mostrará el valor de \hat{\beta}_1 que es el punto de corte con el Eje de la variable Y y el valor de \hat{\beta}_2 que es el parámetro que multiplica a la variable X (también conocido como el peso de la variable).

Esta información puede almacenarse en una variable pues a partir de ella obtener información valiosa sobre nuestro modelo. Entonces, para almacenar esta información en una variable, digamos yx.lm, usamos la siguiente sintaxis:

yx.lm <- lm(Y ~ x)

Veamos la información básica que podemos obtener definiendo del modelo lineal de esta forma.

coefficients

Podemos observar directamente los coeficientes del modelo lineal haciendo el llamado coefficients a partir de la variable que almacena la información del modelo lineal, para esto, recurrimos el símbolo de dólar $ usando la siguiente sintaxis:

yx.lm$coefficients

residuals

Podemos observar directamente los residuos del modelo lineal haciendo el llamado residuals a partir de la variable que almacena la información del modelo lineal, para esto, recurrimos el símbolo de dólar $ usando la siguiente sintaxis: 

yx.lm$residuals

fitted.values

Podemos observar directamente los valores ajustados del modelo lineal, es decir, todos los valores estimados \hat{Y}_i, haciendo el llamado fitted.values a partir de la variable que almacena la información del modelo lineal, para esto, recurrimos el símbolo de dólar $ usando la siguiente sintaxis: 

yx.lm$fitted.values
Anuncios

La instrucción summary()

Si bien se puede obtener información individual haciendo un llamado a algunos elementos específicos del modelo lineal, una de las herramientas más valiosas que provee R para el análisis regresión lineal es el resumen del modelo pues a partir de él, podemos consultar los siguientes elementos:

Sobre el llamado

  • Call – Nos indica la fórmula que define el modelo lineal.

Sobre los residuos

  • Min – Mínimo.
  • 1Q – Primer cuartil Q1.
  • Median – Media (o segundo cuartil Q2)
  • 3Q – Tercer cuartil Q3
  • Max – Máximo.

Es importante verificar que el valor de la media de los residuos sea cero o esté muy cercano a cero, pues este es uno de los supuestos del Método de los Mínimos Cuadrado Ordinarios (MCO).

Sobre los coeficientes

  • Estimate – Estimadores \beta_i.
  • Std. Error – Error estándar de cada estimador.
  • t value – Valor del estadístico t correspondiente a cada estimador.
  • Pr(>|t|) – p-value correspondiente la prueba t de cada estimador.
  • Signif. codes – Códigos de significancia.

En este caso la prueba t plantea la hipótesis nula H_0 : \beta_i = 0, por lo tanto, es importante verificar que el valor t sea lo más grande posible, pues esto nos indica la confianza con la que podemos rechazar la hipótesis nula.

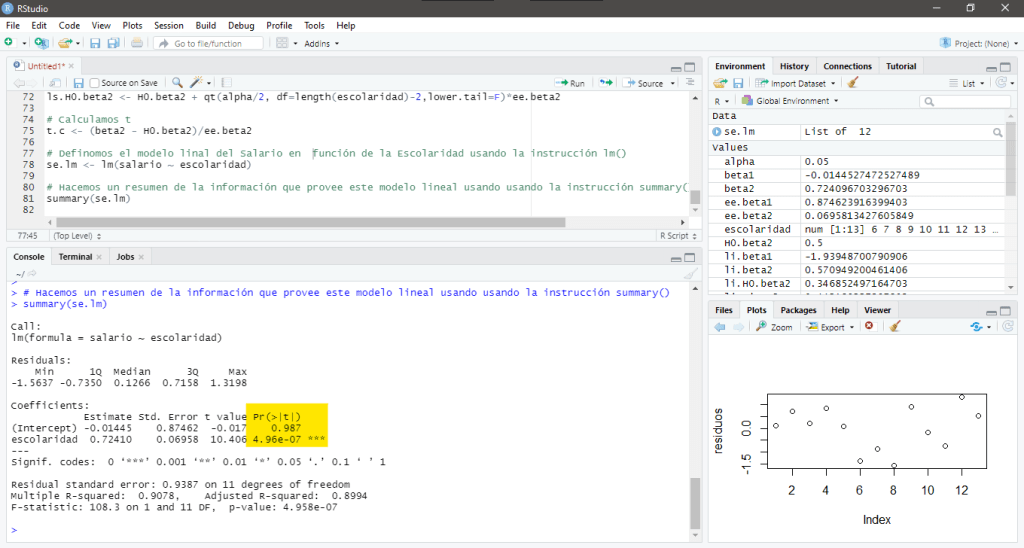
El valor p o p-value determina la probabilidad exacta de cometer un error tipo I considerando el valor t calculado, por lo tanto, es importante verificar que este valor sea lo más bajo posible, pues esto nos indica la confianza con la que podemos rechazar la hipótesis nula.

Para facilitar la interpretación del p-value, se utiliza un código de significancia, notando que

  • 0 ‘***’ La probabilidad de cometer un error tipo I es prácticamente nula.
  • 0.001 ‘**’ La probabilidad de cometer un error tipo I es de a lo sumo el 0.1%.
  • 0.01 ‘*’ La probabilidad de cometer un error tipo I es de a lo sumo el 1%.
  • 0.05 ‘.’ La probabilidad de cometer un error tipo I es de a lo sumo el 5%.
  • 0.1 ‘ ’ La probabilidad de cometer un error tipo I es de a lo sumo el 1%.

Sobre el error estándar de los residuos

  • Residual standard error – Error estándar de estimación o error estándar de la regresión.

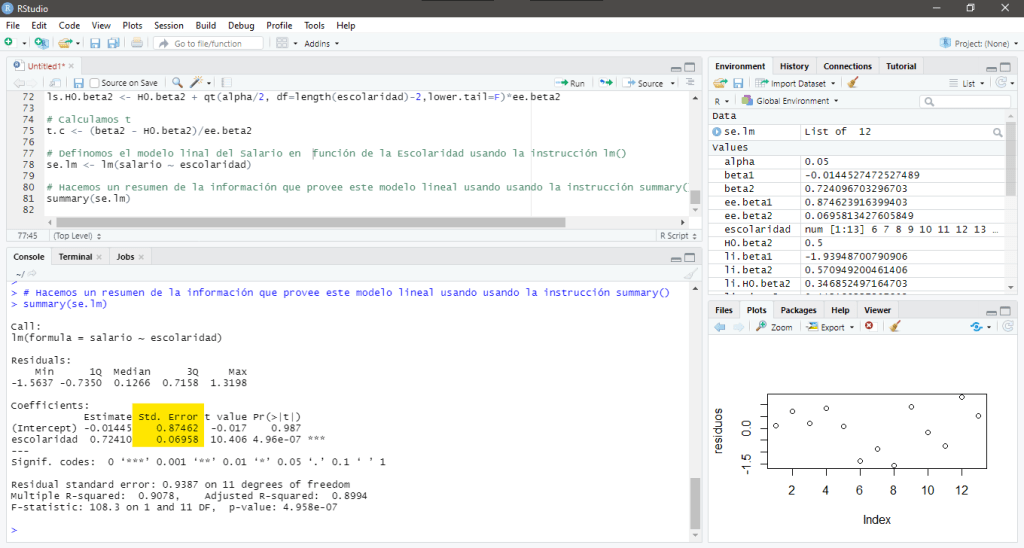
Recordando que el error estándar de estimación nos sirve como una medida de bondad de ajuste, es importante verificar que este sea lo más pequeño posible, recordando siempre que este nunca es igual a cero, pues se define a partir de una suma de cuadrados.

Sobre el coeficiente de determinación

  • Multiple R-squared – Coeficiente de Determinación (sin ajuste al añadir más variables)
  • Adjusted R-squared – Coeficiente de Determinación (con ajuste al añadir más variables)

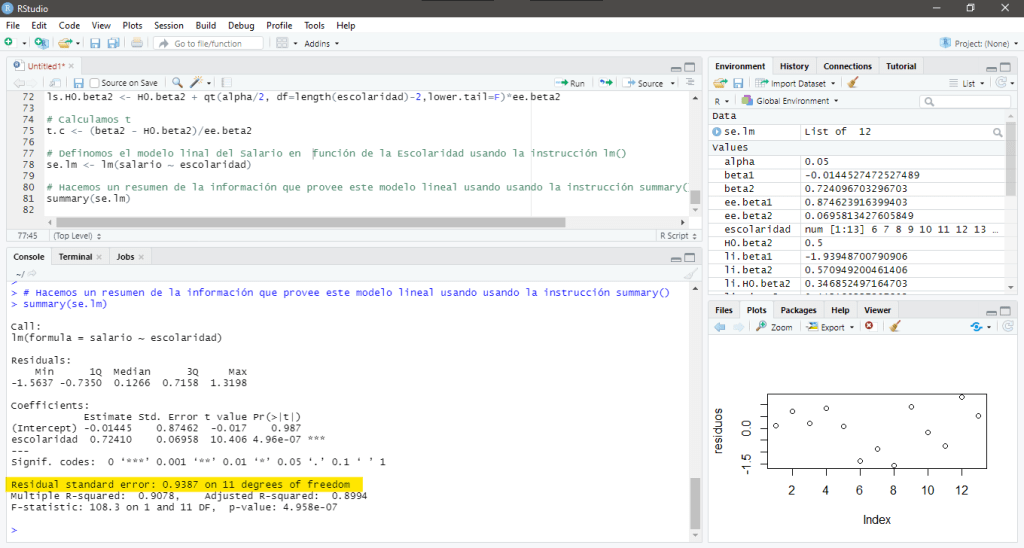
Es importante añadir que al definir modelos, estos no necesariamente se determinan con dos variables, así que al incluir más variables el coeficiente de determinación que determina Multiple R-squared aumentará a medida que se agregan variables, por otra parte, el coeficiente de determinación que determina Adjusted R-squared será corregido por la cantidad de variables involucradas en el modelo por lo que indica de forma más realista en qué medida las variables independientes (en conjunto) explican a la variable dependiente.

Recordemos que si bien es importante que la variable independiente explique la variable pendiente, el objetivo del análisis de regresión no es que el valor del coeficiente de determinación sea igual a 1.

Sobre el estadístico F

  • F-statistic – Estadístico F.

Para el caso de dos variables, la prueba F plantea la hipótesis nula H_0 : \beta_2 = 0, por lo tanto, es importante verificar que el valor F sea lo más grande posible, pues esto nos indica la confianza con la que podemos rechazar la hipótesis nula.

Para el caso de más variables, se plantea una hipótesis conjunta H_0 : \beta_2 = \beta_3 = ... = \beta_k = 0, y de igual forma, es importante verificar que el valor F sea lo más grande posible, pues esto nos indica la confianza con la que podemos rechazar la hipótesis nula.

El valor p o p-value determina la probabilidad exacta de cometer un error tipo I considerando el valor F calculado, por lo tanto, es importante verificar que este valor sea lo más bajo posible, pues esto nos indica la confianza con la que podemos rechazar la hipótesis nula.

Anuncios

Ejemplo

Consideremos un pequeño conjunto de datos, particularmente, los datos que se encuentran en la Tabla 3.2 del libro de Econometría de Damodar N. Gujarati and Dawn Porter en su quinta edición. Este conjunto de datos proporciona los datos primarios que se necesitan para estimar el efecto cuantitativo de la escolaridad en los salarios:

ObservaciónSalarioEscolaridad
14.45676
25.777
35.97878
47.33179
57.318210
66.584411
77.818212
87.835113
911.022314
1010.673815
1110.836116
1213.61517
1313.53118
Tabla 3.2

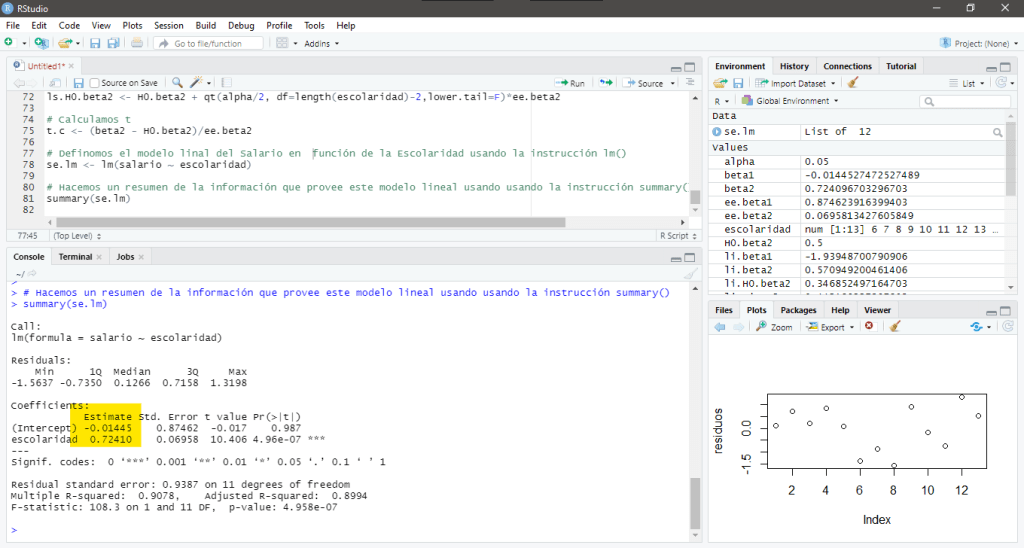
Definimos un modelo lineal que describe el salario en función de la escolaridad con la instrucción lm() y almacenamos esta información en la variable se.lm usando la siguiente sintaxis:

se.lm <- lm(salario ~ escolaridad)

Posteriormente, hacemos un resumen de la información que provee este modelo lineal con la instrucción summary() usando la siguiente sintaxis:

summary(se.lm)

Al ejecutar esta instrucción, inmediatamente aparecerá lo siguiente en la consola:

> summary(se.lm)

Call:
lm(formula = salario ~ escolaridad)

Residuals:
    Min      1Q  Median      3Q     Max 
-1.5637 -0.7350  0.1266  0.7158  1.3198 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -0.01445    0.87462  -0.017    0.987    
escolaridad  0.72410    0.06958  10.406 4.96e-07 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.9387 on 11 degrees of freedom
Multiple R-squared:  0.9078,	Adjusted R-squared:  0.8994 
F-statistic: 108.3 on 1 and 11 DF,  p-value: 4.958e-07

Usualmente el análisis de regresión se enfoca en el coeficiente que acompaña a la variable independiente y le resta importancia a los resultados expuestos sobre el intercepto. Dicho esto, podemos identificar los siguientes elementos en el resumen generado:

  • La media de los residuos es igual a 0.1266, esto es un valor relativamente cercano a cero. Esto es algo que nos interesa pues es uno de los supuestos que debe cumplirse para que el Método de los Mínimos Cuadrados Ordinarios tenga validez.
  • El valor del intercepto es \hat{\beta}_1 = -0.01445, esto quiere decir que una persona sin educación tiene un salario negativo y aunque esta situación carece se sentido, veremos en los demás resultados del resumen, que este valor tiene poca relevancia.
  • El valor del coeficiente que acompaña a la variable X es \hat{\beta}_2 = 0.72410, esto quiere decir que cada año adicional de escolaridad, en promedio, produce aumentos en los salarios por hora de alrededor de 72 centavos de dólar.
  • El modelo lineal está expresado de la siguiente forma:

\hat{Y}_i = -0.01445 + 0.72410 X

  • El error estándar correspondiente al nivel de estudios (escolaridad), indica que en promedio, las estimaciones variarán en 0.06958.
  • El valor t para el estimador \hat{\beta}_1 es igual a -0.017, está muy cercano a cero, esto quiere decir que la hipótesis nula no se rechaza, es decir, el estimador \hat{\beta}_1 no es un elemento significativo en nuestro modelo.
  • El valor t para el estimador \hat{\beta}_2 es igual a 10.406, está muy lejano de cero, por lo tanto la hipótesis nula se rechaza, y así, concluimos que el estimador \hat{\beta}_2 es un elemento bastante significativo en nuestro modelo.
  • El p-value para el estimador \hat{\beta}_1 es igual a 0.987, está muy cercano a uno, esto quiere decir que la hipótesis nula no se rechaza, es decir, el estimador \hat{\beta}_1 no es un elemento significativo en nuestro modelo.
  • El p-value para el estimador \hat{\beta}_2 es prácticamente cero, por lo tanto la hipótesis nula se rechaza, y así, concluimos que el estimador \hat{\beta}_2 es un elemento bastante significativo en nuestro modelo.
  • El error estándar de los residuos es 0.9387, esto quiere decir que cualquier estimación que hagamos variará en 0.9387 centavos de dólar. Proporcionablemente, si comparamos esto con el promedio inicial -0.01445, tenemos que nuestra predicción se desviará en un 65.1875%.
  • El coeficiente de determinación múltiple es igual a 0.9078 y el coeficiente de determinación ajustado es igual a 0.8994, recordemos que este último es corregido por la cantidad de variables y por eso es menor. En ambos casos, es relativamente alto, por lo que podemos concluir que los salarios están explicados en alrededor del 90% por el nivel de escolaridad.
  • El valor F es igual a 108.3, es decir, está muy lejano de uno, por lo tanto la hipótesis nula se rechaza, y así, concluimos que el estimador \hat{\beta}_2 es un elemento bastante significativo en nuestro modelo.
  • El p-value para el estimador \hat{\beta}_2 prácticamente cero, por lo tanto la hipótesis nula se rechaza, y así, concluimos que el estimador \hat{\beta}_2 es un elemento bastante significativo en nuestro modelo.

Bibliografía

R: La prueba t.

Anthonny Arias-García1 comentario

Una vez que hemos aprendido a calcular los intervalos de confianza podemos definir un entorno donde pudiera vivir nuestro parámetro poblacional, sin embargo, es necesario definir un elemento que nos permita usar este entorno para determinar si el planteamiento de nuestra investigación, se ajusta a la estimación que hemos hecho.

La idea básica de las pruebas de significancia es la de definir un estadístico de prueba y su distribución muestral según la hipótesis nula. La decisión de rechazar o no rechazar la hipótesis nula se toma con base en el valor del estadístico de prueba obtenido con los datos disponibles.

También pudiera interesarte

Prueba de significancia de los coeficientes de regresión: la prueba t

Con el supuesto de normalidad de u_i, los estimadores de MCO \hat{\beta}_1 y \hat{\beta}_2 son en sí mismos normalmente distribuidos con sus medias y varianzas correspondientes. Por consiguiente, la variable

t = \dfrac{\hat{\beta}_i - \beta_i}{ee(\hat{\beta}_i)} = \dfrac{(\hat{\beta}_i - \beta_i) \sqrt{\sum x_i^2}}{\hat{\sigma}}

Sigue la distribución t con n - 2 grados de libertad. Si el valor del verdadero \beta_i se especifica con la hipótesis nula, el valor t se calcula fácilmente a partir de la muestra disponible y, por consiguiente, sirve como estadístico de prueba.

Y como este estadístico de prueba sigue una distribución t, caben afirmaciones sobre los intervalos de confianza como la siguiente:

P \left[ -t_{\alpha/2} \leq \dfrac{\hat{\beta}_i - \beta^*_i}{ee(\hat{\beta}_i)} \leq t_{\alpha/2} \right] = 1-\alpha

donde \beta^*_i es el valor de \beta_i que se plantea en la hipótesis nula H_0 y -t_{\alpha/2} y t_{\alpha/2} son los valores de t (los valores críticos de t) obtenidos de la tabla t para un nivel de significancia (\alpha/2) y n-2 grados de libertad.

Reescribiendo la inecuación involucrada, tenemos que

P \left[ \beta^*_i - t_{\alpha/2} ee(\hat{\beta}_i) \leq \hat{\beta}_i \leq \beta^*_i + t_{\alpha/2} ee(\hat{\beta}_i) \right] = 1-\alpha

obteniendo así, el intervalo en el cual se encontrará \hat{\beta}_i con probabilidad 1-\alpha, dado \hat{\beta}_i = \beta^*_i.

Calculamos los valores críticos en R usando la siguiente sintaxis:

li.H0.betai <- betai - qt(alpha/2, df=length(escolaridad)-2,lower.tail=F)*ee.betai
ls.H0.betai <- betai + qt(alpha/2, df=length(escolaridad)-2,lower.tail=F)*ee.betai

En el lenguaje de pruebas de hipótesis, este intervalo de confianza a 100(1 -\alpha)\% se conoce como la región de no rechazo (de la hipótesis nula H_0), y la región que queda fuera del intervalo de confianza conoce como región de rechazo (de la hipótesis nula H_0) o región crítica.

Prueba de Hipótesis, estadístico t | totumat.com

Los límites de confianza dados por los puntos extremos del intervalo de confianza se llaman también valores críticos.

Ahora se aprecia la estrecha conexión entre los enfoques de intervalo de confianza y prueba de significancia para realizar pruebas de hipótesis, pues al compararlos, tenemos que:

En el enfoque de intervalo de confianza se trata de establecer un rango o intervalo que tenga una probabilidad determinada de contener al verdadero aunque desconocido \beta_i

P \left[ \hat{\beta}_i - t_{\alpha/2} ee(\hat{\beta}_i) \leq \beta_i \leq \hat{\beta}_i + t_{\alpha/2} ee(\hat{\beta}_i) \right] = 1-\alpha

En el enfoque de prueba de significancia se somete a hipótesis algún valor de \beta_i y se ve si el estimador \hat{\beta}_i calculado se encuentra dentro de los límites (de confianza) razonables alrededor del valor sometido a hipótesis.

P \left[ \beta^*_i - t_{\alpha/2} ee(\hat{\beta}_i) \leq \hat{\beta}_i \leq \beta^*_i + t_{\alpha/2} ee(\hat{\beta}_i) \right] = 1-\alpha

Sin embargo, en la práctica, no hay necesidad de estimar este intervalo explícitamente. Se calcula el valor de t y se ve si cae entre los valores críticos t o fuera de ellos y calculamos el valor de t en R usando la siguiente sintaxis:

t.c <- (betai - H0.betai)/ee.betai
Prueba de Hipótesis, estadístico t | totumat.com

Ejemplo

Consideremos un pequeño conjunto de datos, particularmente, los datos que se encuentran en la Tabla 3.2 del libro de Econometría de Damodar N. Gujarati and Dawn Porter en su quinta edición. Este conjunto de datos proporciona los datos primarios que se necesitan para estimar el efecto cuantitativo de la escolaridad en los salarios:

ObservaciónSalarioEscolaridad
14.45676
25.777
35.97878
47.33179
57.318210
66.584411
77.818212
87.835113
911.022314
1010.673815
1110.836116
1213.61517
1313.53118
Tabla 3.2

Sabiendo que \hat{\beta}_2 = 0.7240, ee(\hat{\beta}_2) = 0.0700 y gl=11. Si consideramos \alpha=5\%, entonces t_{\alpha/2}=2.201.

Considerando la hipótesis nula H_0 : \beta_2 = \beta_2^* = 0.5 y la hipótesis alternativa H_1:\beta_2 \neq 0.5, calculamos los valores críticos en R usando la siguiente sintaxis:

H0.beta2 <- 0.5
li.H0.beta2 <- H0.beta2 - qt(alpha/2, df=length(escolaridad)-2,lower.tail=F)*ee.beta2
ls.H0.beta2 <- H0.beta2 + qt(alpha/2, df=length(escolaridad)-2,lower.tail=F)*ee.beta2

Una vez ejecutadas estas instrucciones, obtenemos que

P (0.3460 \leq \hat{\beta}_2 \leq 0.6540) = 1-\alpha

De forma gráfica, podemos expresar esta probabilidad así

Prueba de Hipótesis, estadístico t | totumat.com

Notamos entonces, que el valor \hat{\beta}_2 = 0.7240 está en la región de rechazo, por lo tanto, se rechaza la hipótesis nula H_0.

Veamos ahora, qué es lo que ocurre con el valor que hemos calculado de t. ¿Cae entre los valores críticos t o fuera de ellos? t = \frac{0.7240 - 0.5}{0.0700} = 3.2. Calculamos el valor de t en R usando la siguiente sintaxis:

H0.beta2 <- 0.5
t.c <- (beta2 - H0.beta2)/ee.beta2

En el siguiente gráfico, vemos con claridad que el valor se encuentra en la región crítica y la conclusión se mantiene; es decir, rechazamos H_0.

Prueba de Hipótesis, estadístico t | totumat.com

En su pantalla debería aparecer:

Prueba de Hipótesis, estadístico t | totumat.com

Notas:

Observe que si el \beta_i estimado es igual al \beta_i hipotético, el valor t será cero. Por otra parte, a la medida en que el valor de \beta_2 estimado se aleje del valor hipotético de \beta_2, el |t| será cada vez mayor. Por consiguiente, un valor grande de |t| nos permite rechazar la hipótesis nula con mayor confianza.

En la práctica, se plantea la hipótesis nula H_0 : \beta_i (con énfasis en beta_2) pues al rechazar esta hipótesis, podemos asegurar con cierto grado de confianza, que beta_2 \neq 0 y así, concluir que la variable que acompaña a beta_2 explica a la variable dependiente.