Proceda paso a paso, explicando detalladamente cada paso con sus propias palabras.
Verifique si el límite correspondiente es indeterminado o no, en caso de ser indeterminado, aplique que la técnica correspondiente para determinarlo.

Proceda paso a paso, explicando detalladamente cada paso con sus propias palabras.
Verifique si el límite correspondiente es indeterminado o no, en caso de ser indeterminado, aplique que la técnica correspondiente para determinarlo.

Hasta ahora hemos estudiado el límite de las operaciones básicas entre funciones, sin embargo, si consideramos dos funciones y
, entonces la función
cuando
tiende a infinito debe calcularse tomando tomando en cuenta que
está indeterminado.
La técnica para determinar este tipo de límites parte de la definición del número y es que podemos notar que si hacemos una simple sustitución en el siguiente límite, podemos notar que éste presenta una indeterminación
Afortunadamente, sabemos que éste límite define justamente al número , entonces
Esta fórmula se puede generalizar aún más, pues si consideramos una función que tiende a infinito cuando
tiende a infinito, entonces
De esta forma, al toparnos con la indeterminación puede ser conveniente reescribir la expresión que define la función para obtener el número. Veamos en los siguientes ejemplos como determinar este tipo de límites.
Si consideramos , este límite presenta una indeterminación. Notamos que este límite es levemente diferente al límite que define el número
, así que tomando en cuenta la propiedad de las potencias
entonces podemos reescribir el límite para encontrar la definición del número
de la siguiente forma
De esta forma, notamos que la expresión que está dentro de los corchetes es la definición del número , entonces al calcular el límite obtenemos
Por lo tanto, concluimos que
De forma general, si consideramos una función que tiende a infinito cuando
tiende a infinito, entonces
Si consideramos , este límite presenta una indeterminación. Podemos reescribir de la siguiente forma
De esta forma, notamos que la expresión que está dentro de los corchetes es la definición del número , entonces al calcular el límite obtenemos
Por lo tanto, concluimos que
Si consideramos , este límite presenta una indeterminación. Reescribimos el límite de la siguiente forma
De esta forma, notamos que la expresión que está dentro de los corchetes es la definición del número , entonces al calcular el límite obtenemos
Por lo tanto, concluimos que
Si consideramos , este límite presenta una indeterminación. Reescribimos el límite de la siguiente forma
De forma general, si consideramos dos funciones y
tales que
tiende a infinito cuando
tiende a infinito, entonces
Si consideramos , este límite presenta una indeterminación. Notamos a diferencia del ejemplo anterior, la solución no es tan simple como separar las sumas de fracciones. Así que reescribimos sumando y restando uno en el límite de la siguiente forma
Efectuamos la suma de fracciones para obtener
Ahora multiplicamos y dividimos en el exponente por los factores y
para luego conservar la expresión de nuestro interés,
Aplicamos entonces las propiedades de la potencia de la siguiente manera y obtenemos
Notando que la expresión que está dentro de los corchetes es la definición del número y considerando que en el exponente el polinomio en el numerador y el polinomio en el denominador tienen el mismo grado, el límite será igual al cociente entre sus coeficientes principales, entonces al calcular el límite el resultado será
Por lo tanto, concluimos que
Este tipo de límites no presentan mayor complicación al calcularlos y aunque esta técnica es bastante amplia, encontraremos ocasiones en las que podemos recurrir a métodos más sofisticados pues la técnica que hemos usado hasta ahora puede resultar engorrosa. Veamos entonces, la siguiente serie de igualdades para determinar una fórmula que nos permita calcular este tipo de límites.
Por lo tanto, tenemos que
Veamos en los siguientes ejemplos como determinar este tipo de límites.
Si consideramos , este límite presenta una indeterminación. Entonces, aplicando la fórmula, tenemos que
Entonces, basta con determinar el límite , para esto efectuamos la suma de fracciones para obtener
Posteriormente efectuamos el producto entre los numeradores aplicando la propiedad distributiva, y obtenemos
Y considerando que el polinomio en el numerador y el polinomio en el denominador tienen el mismo grado, el límite será igual al cociente entre sus coeficientes principales, es decir, . Por lo tanto, concluimos que
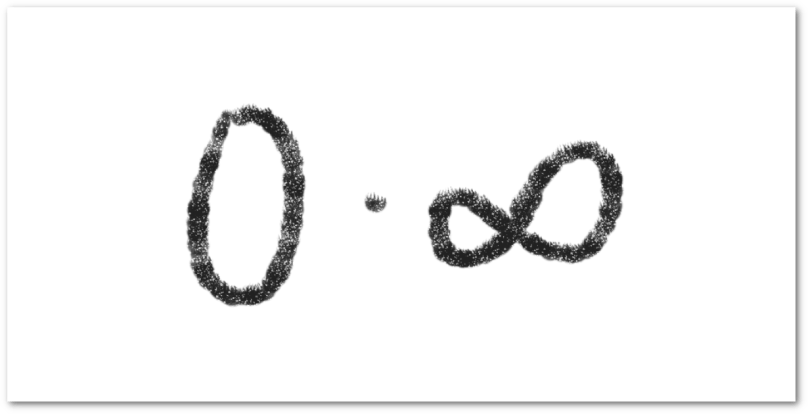
Si y
son dos funciones cuyos límites tienden a infinito y a cero, respectivamente cuando
tiende al infinito, entonces el límite del producto de estas dos funciones presenta una indeterminación. La forma en que se determinan este tipo de límites consiste en reescribir la expresión para obtener una indeterminación de la forma
y usar las técnicas usadas para estos casos. Veamos en los siguientes ejemplos como determinar este tipo de límites
Si consideramos , este presenta una indeterminación. Multiplicamos el producto entre las fracciones y posteriormente aplicamos la técnica que hemos visto anteriormente
Y al evaluar el límite obtenemos
Por lo tanto, concluimos que
Si consideramos , este presenta una indeterminación. Efectuamos la suma de fracciones para obtener
Posteriormente efectuamos el producto entre los numeradores aplicando la propiedad distributiva, y obtenemos
Y considerando que el polinomio en el numerador y el polinomio en el denominador tienen el mismo grado, el límite será igual al cociente entre sus coeficientes principales, por lo tanto, concluimos que
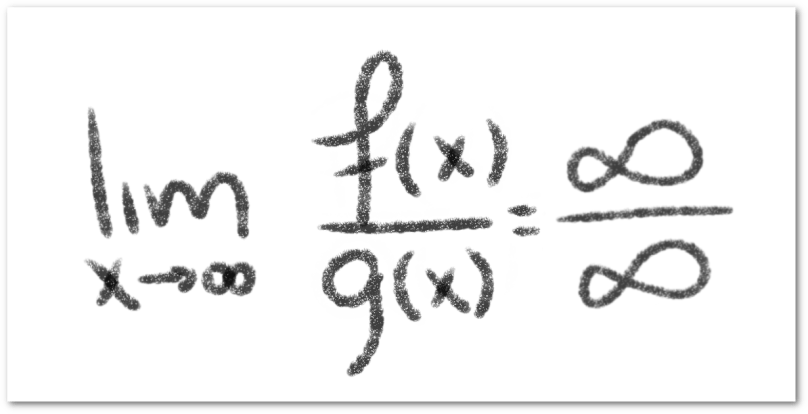
Vimos que al considerar el cociente entre polinomios cuando la variable tiende infinito, se puede determinar el límite considerando el grado de los polinomios. Esta situación se puede generalizar para cualquier cociente entre funciones considerando el grado de ambas funciones. Veamos entonces con los siguientes ejemplos como determinar este tipo de límites.
También pudiera interesarte
Si consideramos , este límite presenta una indeterminación pero considerando que el grado de la función en el numerador es igual a
y el grado del denominador es igual a
entonces
Si consideramos , este límite presenta una indeterminación pero considerando que el grado de la función en el numerador es exponencial y el grado del denominador es igual a
entonces
Si consideramos , este límite presenta una indeterminación pero considerando que el grado de la función en el numerador es igual a 1 y el grado del denominador es logarítmico entonces
Si bien estos ejemplos no presentan mayor complicación para determinarlos debido a que la diferencia entre los grados es clara, vale la pena considerar otros ejemplos en los que el grado de las funciones es el mismo. La técnica no será muy distinta a la que usamos para determinar los límites de cocientes entre polinomios pues dividiremos siempre el numerador y el denominador por la función elemental de mayor grado involucrada en el límite.
Si consideramos , este límite presenta una indeterminación pero considerando que el grado en ambos miembros de la fracción es
, entonces dividimos el numerador y el denominador por
Una vez que hemos dividido, separamos la suma en los numeradores de cada fracción de la siguiente forma
Notamos además, que podemos combinar las raíces cuadradas de la siguiente manera
Simplificamos entonces cada una de las fracciones generadas de la misma forma que las hemos simplificado anteriormente, para obtener
Calculamos entonces el límite de cada uno de las expresiones involucradas, teniendo en cuenta que y
(con
), así el límite será igual a
Por lo tanto concluimos que
Al considerar funciones algebraicas es más intuitiva la simplificación de las expresiones, sin embargo, al considerar funciones trascendentales esta simplificación no es tan obvia, es por eso que en los siguientes ejemplos veremos algunos casos donde podemos determinar los límites de forma intuitiva.
Si consideramos , este límite presenta una indeterminación pero considerando que el grado en ambos miembros de la fracción es exponencial, entonces dividimos el numerador y el denominador por
Una vez que hemos dividido, separamos la suma en los numeradores de cada fracción de la siguiente forma
Simplificamos entonces cada una de las fracciones generadas, para obtener
Calculamos entonces el límite de cada uno de los sumandos involucrados, teniendo en cuenta que (con
),
y
, así el límite será igual a
Por lo tanto concluimos que
Si consideramos , este límite presenta una indeterminación pero considerando que el grado en ambos miembros de la fracción es exponencial, entonces dividimos el numerador y el denominador por
Una vez que hemos dividido, separamos la suma en los numeradores de cada fracción de la siguiente forma
Simplificamos entonces cada una de las fracciones generadas, para obtener
Calculamos entonces el límite de cada uno de los sumandos involucrados, teniendo en cuenta que (con
), así el límite será igual a
Por lo tanto concluimos que

Si y
son dos funciones cuyos límites tienden a infinito cuando
tiende al infinito, entonces el límite de la división entre estas dos funciones presenta una indeterminación
Consideremos de forma particular en el que y
son funciones polinomiales que tienden a infinito cuando
tiende a infinito. El método para determinar este tipo de límites consiste en dividir por
en el numerador y en el denominador, donde
es el mayor grado involucrado en el límite. Veamos con algunos ejemplos como desarrollar este método.
También pudiera interesarte
Si consideramos , este límite presenta una indeterminación pero considerando que
es el mayor grado involucrado en el límite, entonces dividimos en el numerador y en el denominador por
.
Una vez que hemos dividido, separamos la suma en los numeradores de cada fracción de la siguiente forma
Simplificamos entonces cada una de las fracciones generadas, para obtener
Calculamos entonces el límite de cada uno de los sumandos involucrados, teniendo en cuenta que ,
, así el límite será igual a
Donde la fracción servirá como indicador de que el numerador crece con mayor velocidad que el denominador, por lo tanto concluimos que
.
\item Si consideramos , este límite presenta una indeterminación pero considerando que
es el mayor grado involucrado en el límite, entonces dividimos en el numerador y en el denominador por
.
Una vez que hemos dividido, separamos la suma en los numeradores de cada fracción de la siguiente forma
Simplificamos entonces cada una de las fracciones generadas, para obtener
Calculamos entonces el límite de cada uno de los sumandos involucrados, teniendo en cuenta que , así el límite será igual a
Por lo tanto concluimos que .
Si consideramos , este límite presenta una indeterminación pero considerando que
es el mayor grado involucrado en el límite, entonces dividimos en el numerador y en el denominador por
.
Una vez que hemos dividido, separamos la suma en los numeradores de cada fracción de la siguiente forma
Simplificamos entonces cada una de las fracciones generadas, para obtener
Calculamos entonces el límite de cada uno de los sumandos involucrados, teniendo en cuenta que , así el límite será igual a
Donde la fracción servirá como indicador de que el denominador crece con mayor velocidad que el numerador, por lo tanto concluimos que
.
Considerando estos tres últimos ejemplos, podemos notar que si consideramos dos polinomios que están definidos de la siguiente forma:
Entonces, el límite de la división cuando
tiende a infinito estará determinado de la siguiente forma:
Debe estar conectado para enviar un comentario.