Etiqueta: Aplicaciones en la Economía

Función de Costos Conjuntos

Anthonny Arias-García1 comentario

Suponga que un fabricante produce x unidades de un artículo X y y unidades de un artículo Y, entonces el costo total de producir esas unidades se puede expresar como una función c que depende de las variables x y y, que llamaremos Función de Costos Conjuntos y la denotaremos de la siguiente forma

c(x,y)

También pudiera interesarte

Una vez que fijamos la producción del producto Y, podemos calcular la razón de cambio de los costos conjuntos respecto al producto X calculando la derivada parcial de la función c(x,y) respecto a x, es decir, la función de costo marginal respecto a la variable x

\dfrac{\partial c}{\partial x}

Por ejemplo, si c se expresa en perolitos y \frac{\partial c}{\partial x} = 1500, entonces el costo de producir una unidad adicional de X cuando el nivel de producción de Y es fijo, es aproximadamente de 1500 perolitos.

Nota: Perolitos (Ps.) es la moneda oficial de totumat.

En cambio, si fijamos la producción del producto X, podemos calcular la razón de cambio de los costos conjuntos respecto al producto Y calculando la derivada parcial de la función c(x,y) respecto a y, es decir, la función de costo marginal respecto a la variable y

\dfrac{\partial c}{\partial y}

Por ejemplo, si c se expresa en perolitos y \frac{\partial c}{\partial y} = 2000, entonces el costo de producir una unidad adicional de Y cuando el nivel de producción de X es fijo, es aproximadamente de 1500 perolitos.

Aunque durante este clase nos limitaremos a dos variables, pero de forma general si un fabricante produce n artículos entonces la función de costos conjuntos constará de n variables y habrá n funciones de costo marginal.

Anuncios

Ejemplo

Una empresa produce Plátano Chips de dos sabores: salado y natural. Suponga que la función de costos conjuntos de producir x empaques de plátano chips salados y y empaques de plátano chips naturales es:

c(x,y)=0.07x^2 +75x+85y+600

Donde c se expresa en perolitos.

Determine los costos marginales de c respecto a x y y cuando x=100 y y=50, finalmente interprete los resultados.

Para esto, calculamos la derivada parcial de la función c respecto a x.

\dfrac{\partial c}{\partial x} = 0.14x+75

y evaluando esta función en el punto (100,50) obtenemos:

\left. \dfrac{\partial c}{\partial x} \right|_{(100,50)} = 0.14(100)+75 = 89

Por lo tanto, al aumentar la producción de plátano chips saladas de 100 a 101 mientras se mantiene fija la producción de chips naturales en 50, los costos conjuntos aumentan aproximadamente en 89 Ps.

Por otra parte, calculamos la derivada parcial de la función c respecto a y.

\dfrac{\partial c}{\partial y} = 85

y evaluando esta función en el punto (100,50) obtenemos:

\left. \dfrac{\partial c}{\partial y} \right|_{(100,50)} = 85

Por lo tanto, al aumentar la producción de plátano chips naturales de 50 a 51 mientras se mantiene fija la producción de chips saladas en 100, los costos conjuntos aumentan aproximadamente en 85 Ps.

Coronavirus – COVID-19 (Un enfoque matemático)

Anthonny Arias-García2 comentarios

¿Qué es el coronavirus?

Ante las noticias sobre un nuevo brote del coronavirus es pertinente que todos estemos al tanto sobre lo referente a este virus. La Organización Mundial de la Salud (OMS) comparte la siguiente información en su página web:

Los coronavirus son una extensa familia de virus, algunos de los cuales pueden ser causa de diversas enfermedades humanas, que van desde el resfriado común hasta el SRAS (síndrome respiratorio agudo severo). Los virus de esta familia también pueden causar varias enfermedades en los animales.

¿Cuáles son los síntomas del coronavirus?

La agencia de noticias Deutsche Welle (DW) informa los siguientes síntomas:

Los pacientes que han contraído el virus han tenido fiebre, dificultad para respirar y tos. El virus también puede causar neumonía, una infección que inflama los sacos de aire en los pulmones y puede hacer que se llenen de líquido o pus. Los ciudadanos mayores tienden a verse más afectados por el virus que las personas más jóvenes.

¿Un nuevo coronavirus?

En el portal de The Guardian, indican qué es lo que ha ocurrido en Wuhan, la extensa capital de la provincia de Hubei en China central donde el virus ha tomado más vidas:

Es un nuevo coronavirus, es decir, un miembro de la familia de los coronavirus que nunca antes se había encontrado. Al igual que otros coronavirus, proviene de animales. Muchos de los infectados trabajaban o compraban frecuentemente en el mercado mayorista de mariscos de Huanan en el centro de la ciudad china, que también vendía animales vivos y recién sacrificados. Los virus nuevos y problemáticos generalmente se originan en huéspedes animales. El ébola y la gripe son ejemplos.

¡La simulación!

Por otra parte, Business Insider va directo a los números y contacta a Eric Toner, científico del Centro Johns Hopkins para la Seguridad de la Salud quién llevó a cabo una simulación de propagación del coronavirus tres meses antes del brote en el Evento 201. La simulación de Toner de una hipotética pandemia mortal de coronavirus sugirió que después de seis meses, casi todos los países del mundo tendrían casos del virus. En 18 meses, 65 millones de personas podrían morir.

Si bien Toner pudo con la tecnología de hoy en día simular una pandemia, este poder de cómputo no siempre ha estado disponible. Sin embargo, el estudio sobre la propagación de enfermedades ha ocupado —y preocupado— a los científicos de todas las eras y particularmente a los matemáticos.

El modelo matemático

Daniel Bernoulli, un matemático y físico suizo, realizó la primera aplicación de ecuaciones diferenciales al estudio de epidemias y enfermedades contagiosas en el año 1760. Y aunque este modelo se ha refinado con el tiempo, tal como lo presentan Dietz K y Heesterbeek JA en su artículo Daniel Bernoulli’s epidemiological model revisited, o modelos como el que presenta Tom Britton de la Universidad de Estocolmo en su artículo Stochastic epidemic models: a survey. Este modelo ilustra la línea de pensamiento que planteó Bernoulli:

La enfermedad en cuestión es la viruela. La enfermedad es contagiosa, pero confiere inmunidad completa a cualquiera que la haya contraído y se haya recuperado. Es esta última característica la que hace que la vacunación sea tan efectiva y finalmente hizo posible erradicar la enfermedad.

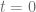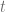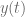Bernoulli comienza con una población de personas en el momento t = 0. Suponga que en el momento t hay x(t) personas vivas y y(t) personas vivas que aún no han tenido viruela. El modelo es

Donde a es la tasa de que la y-población es susceptible a la enfermedad, b (con 0 < b < 1) es la fracción de la y-población que contrae la enfermedad y no se recupera, y d(t) es la tasa de mortalidad de todas las demás enfermedades. Multiplicando la primera ecuación por 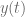y(t) y la segunda por x(t), obtenemos

De esta forma, al restar ambas ecuaciones se cancelan los sumandos 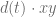d(t) \cdot xy y así

Entonces, si consideramos la variable auxiliar z=\dfrac{x}{y}, ésta última ecuación se puede reescribir como

z' = -ab + az \Rightarrow z' - az = -ab

Que es una ecuación diferencial ordinaria lineal no-homogénea de primer orden, que podemos calcular definiendo su factor integrante. Notando que P(t)=-a, entonces \mu(t) = \text{\Large e}^{\int -a dt} = \text{\Large e}^{-at} , por lo tanto

Al considerar el problema de valor inicial 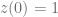z(0)=1, entonces la solución de la ecuación diferencial que cumple con esta condición está expresada de la siguiente manera:

z = b + (1-b) \text{\Large e}^{at}

Bernoulli estimó que 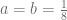a=b=\frac{1}{8} después de estudiar tablas de mortalidad, así que recomendó la vacunación.

¿Cómo prevenirlo?

Actualmente se sabe que este virus se contagia de humano a humano y, aunque no está clara la forma en que se contagia, las siguientes indicaciones son normales generales para prevenir cualquier enfermedad de contacto o por vías respiratorias.

  • Lave sus manos con agua y jabón frecuentemente.
  • Evite tocarse la boca, nariz u ojos; principalmente si se encuentra en la calle.
  • Tape su boca cuando tosa y si lo hace, no estreche la mano con otras personas.
  • Si presenta síntomas de estar enfermo, use tapabocas para evitar que otras personas se enfermen.
  • Use tapabocas si va a lugares muy concurridos, pues es en esos casos aumenta la probabilidad de contagio.

El Modelo de Bernoulli tomado del libro Elementary Differential Equations de C. Henry Edwards, David E. Penney en su sexta edición.