Las grandes constantes matemáticas
Las grandes constantes matemáticas provienen en su mayoría de relaciones geométricas por ejemplo, la constante de Pitágoras es la longitud de la hipotenusa de un triángulo rectángulo con ambos catetos igual a
,
es la proporción de la longitud de arco de una circunferencia entre su diámetro y el número de oro
que define la proporción áurea (dos cantidades están en la proporción áurea si su proporción es igual a la proporción de su suma a la mayor de las dos cantidades).

Sin embargo, otras constantes que no provienen de este tipo de relaciones.
El interés compuesto
Suponga que usted invierte un capital en un banco que ofrece un plan de plazo fijo con una tasa de interés compuesto del
anual. Entonces, Al final del primer año usted habrá acumulado lo que tenía en el año anterior (
) más un
por ciento de ese capital (
), es decir,
Y notando que podemos sacar a como un factor común, obtenemos
Al final del segundo año usted habrá acumulado lo que tenía en el año anterior () más un
por ciento de ese capital (
), es decir,
Y notando que podemos sacar a como un factor común, obtenemos
Si continuamos razonando de esta manera, podemos concluir que al final del tercer año usted habrá acumulado , al final del cuarto año
y así de forma sucesiva, podemos decir que al final del n-ésimo año habrá acumulado
Un caso particular
Esta fórmula nos provee una forma general de calcular el capital acumulado con una tasa de interés al cabo de
periodos de tiempo. Consideremos un caso muy particular, en el que tomamos un perolito (moneda oficial de totumat) y los invertimos en un banco que ofrece una tasa de interés del 100% anual. Entonces, al cabo de un año habremos acumulado
Supongamos ahora que este banco, ofrece una tasa de interés del 50% semestral, de esta forma, al final del año han culminado dos periodos y así, habremos acumulado
Notamos que al final del año se habrá acumulado un capital mayor por lo que parece atractiva la idea de segmentar el año más cuotas de interés, entonces si consideramos una tasa de interés del 33.333% cuatrimestral, al final del año han culminado tres periodos y así, habremos acumulado
Podemos razonar de esta manera de forma sucesiva, partiendo el año en periodos más pequeños para maximizar nuestro capital acumulado, sin embargo, observemos cuidadosamente lo que ocurre
Si bien el capital acumulado aumenta a medida que segmentamos el año, éste tiende a estancarse incluso si estamos acumulando intereses de forma continua en el tiempo. Lo que que han descubierto las matemáticas es que a medida que tiende a infinito, la expresión
tiende a un número particular que se conoce como la Constante de Euler o Constante de Napier. De forma general, tenemos que
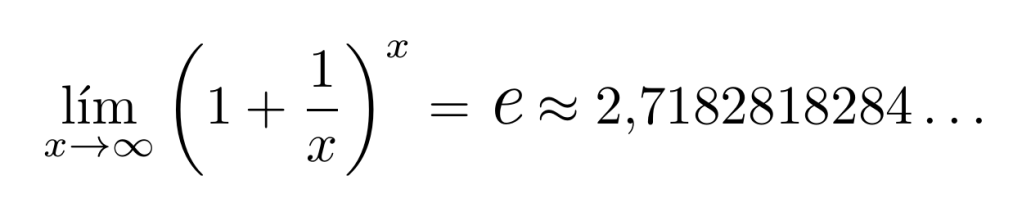
El número tiene gran importancia en las matemáticas ya que este representa el crecimiento natural de las cosas. Además cuenta con propiedades muy ricas en el cálculo diferencial e integral.
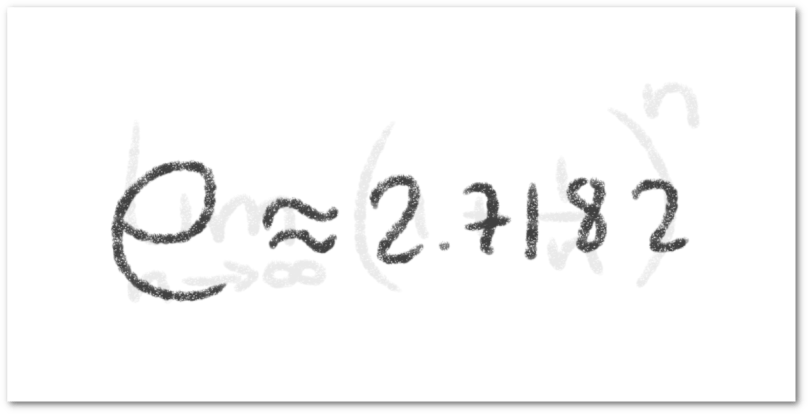


Debe estar conectado para enviar un comentario.