- La Sintaxis de LaTeX
- La Sintaxis de LaTeX en WordPress
- Cambiando el tamaño
- Cambiando los colores
- WordPress Latex Shortcode
En el mundo de las matemáticas, el lenguaje que se usa, requiere de caracteres y símbolos especiales que si bien, al escribir a mano, estos se pueden hacer incluso con un solo trazo; al escribir en una computadora, debemos recurrir a herramientas especiales. Una de estas herramientas especiales es 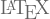 , que nos permite a través de un lenguaje de entornos, escribir caracteres y símbolos matemáticos.
, que nos permite a través de un lenguaje de entornos, escribir caracteres y símbolos matemáticos.
Nuestra web totumat.com está construida sobre WordPress y el uso de 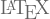 es vital para escribir todos sus contenidos; pese a que la documentación sobre el uso de
es vital para escribir todos sus contenidos; pese a que la documentación sobre el uso de 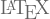 es extensa, en esta publicación no veremos en detalle el uso de las instrucciones para escribir caracteres y símbolos especiales, en cambio veremos cómo usar las herramientas que provee WordPress para usar el lenguaje de
es extensa, en esta publicación no veremos en detalle el uso de las instrucciones para escribir caracteres y símbolos especiales, en cambio veremos cómo usar las herramientas que provee WordPress para usar el lenguaje de 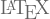 en el texto de los bloques.
en el texto de los bloques.
También pudiera interesarte
La Sintaxis de LaTeX
Cualquier documento de 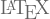 tiene un preámbulo en el que se definen los parámetros con los que se generará el documento, por lo que es importante, definir la forma en que el lenguaje matemático se escribirá. WordPress generará los caracteres y símbolos especiales utilizando los siguientes paquetes:
tiene un preámbulo en el que se definen los parámetros con los que se generará el documento, por lo que es importante, definir la forma en que el lenguaje matemático se escribirá. WordPress generará los caracteres y símbolos especiales utilizando los siguientes paquetes:
Al escribir en editores de texto tales como TeXworks u Overleaf, obtenemos un resultado limpio y detallado basado en vectores, generalmente impreso digitalmente en formato PDF. La escritura de caracteres y símbolos matemáticos, se puede ejecutar de dos formas:
- En la línea (inline math): se deben encerrar las instrucciones entre los siguientes entornos
$ $
ó
\( \)
- Desplegado (display math): se deben encerrar las instrucciones entre los siguientes entornos:
$$ $$
ó
\[ \]
De esta forma, si escribimos el siguiente texto:
Al considerar la ecuación cuadrática: $x^2+5x+6=0$, debemos notar que el término $x^2$ no tiene antepuesto ningún coeficiente, esto quiere decir que está multiplicado por uno, ya que $x^2 = 1 \cdot x^2$. Así, tenemos que $a=1$, $b=5$ y $c=6$. Entonces,
$$x = \dfrac{-b \pm \sqrt{b^2-4 \cdot a \cdot c}}{2 \cdot a}$$
$$= \dfrac{-5 \pm \sqrt{5^2-4 \cdot 1 \cdot 6}}{2 \cdot 1}$$
Obtenemos el siguiente resultado:
La Sintaxis de LaTeX en WordPress
Al escribir en WordPress, obtenemos un resultado tosco y de baja calidad basado en imágenes, impresas en la web en formato PNG. La escritura de caracteres y símbolos matemáticos, también se puede ejecutar de dos formas:
- En la línea (inline math): se deben encerrar las instrucciones entre el siguiente entorno
$latex $
- Desplegado (display math): se usa la instrucción \displaystyle una vez que se abre el entorno de la siguiente forma:
$latex \displaystyle $
Hay que destacar que el código corto se debe usar sólo una vez en un bloque o usar un bloque dedicado para que no haya conflicto con los entornos.
De esta forma, si escribimos el siguiente texto:
Al considerar la ecuación cuadrática: $latex x^2+5x+6=0$, debemos notar que el término $latex x^2$ no tiene antepuesto ningún coeficiente, esto quiere decir que está multiplicado por uno, ya que $latex x^2 = 1 \cdot x^2$. Así, tenemos que $latex a=1$, $latex b=5$ y $latex c=6$. Entonces,
$latex \displaystyle x = \dfrac{-b \pm \sqrt{b^2-4 \cdot a \cdot c}}{2 \cdot a}$
$latex \displaystyle = \dfrac{-5 \pm \sqrt{5^2-4 \cdot 1 \cdot 6}}{2 \cdot 1}$
Obtenemos el siguiente resultado:
Al considerar la ecuación cuadrática:  ., debemos notar que el término
., debemos notar que el término 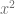 no tiene antepuesto ningún coeficiente, esto quiere decir que está multiplicado por uno, ya que
no tiene antepuesto ningún coeficiente, esto quiere decir que está multiplicado por uno, ya que  . Así, tenemos que
. Así, tenemos que  ,
, 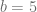 y
y  . Entonces,
. Entonces,

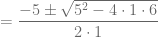
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Cambiando el tamaño
Es posible cambiar el tamaño de los caracteres y símbolos especiales que genera WordPress, pues en ocasiones resulta necesario escribirlo más grande o más pequeño. Basta con usar la instrucción &s=[tamaño] antes de cerrar el entorno, donde «[tamaño]» es un número que varía desde -4 equivalente al tamaño \tiny en LaTeX hasta 4 correspondiente al tamaño \huge en LaTeX.
Entonces si escribimos lo siguiente:
$latex \dfrac{-b \pm \sqrt{b^2-4 \cdot a \cdot c}}{2 \cdot a} &s=-4$
Donde -4 es el tamaño equivalente al tamaño \tiny en LaTeX. Obtenemos el siguiente resultado:

$latex \dfrac{-b \pm \sqrt{b^2-4 \cdot a \cdot c}}{2 \cdot a} &s=-3$
Donde -3 es el tamaño equivalente al tamaño \scriptsize en LaTeX. Obtenemos el siguiente resultado:

$latex \dfrac{-b \pm \sqrt{b^2-4 \cdot a \cdot c}}{2 \cdot a} &s=-2$
Donde -2 es el tamaño equivalente al tamaño \footnotesize en LaTeX. Obtenemos el siguiente resultado:

$latex \dfrac{-b \pm \sqrt{b^2-4 \cdot a \cdot c}}{2 \cdot a} &s=-1$
Donde -1 es el tamaño equivalente al tamaño \small en LaTeX. Obtenemos el siguiente resultado:

$latex \dfrac{-b \pm \sqrt{b^2-4 \cdot a \cdot c}}{2 \cdot a} &s=0$
Donde 0 es el tamaño equivalente al tamaño \normalsize en LaTeX. Obtenemos el siguiente resultado:

$latex \dfrac{-b \pm \sqrt{b^2-4 \cdot a \cdot c}}{2 \cdot a} &s=1$
Donde 1 es el tamaño equivalente al tamaño \large en LaTeX. Obtenemos el siguiente resultado:
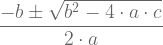
$latex \dfrac{-b \pm \sqrt{b^2-4 \cdot a \cdot c}}{2 \cdot a} &s=2$
Donde 2 es el tamaño equivalente al tamaño \Large en LaTeX. Obtenemos el siguiente resultado:
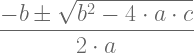
$latex \dfrac{-b \pm \sqrt{b^2-4 \cdot a \cdot c}}{2 \cdot a} &s=3$
Donde 3 es el tamaño equivalente al tamaño \LARGE en LaTeX. Obtenemos el siguiente resultado:
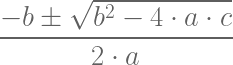
$latex \dfrac{-b \pm \sqrt{b^2-4 \cdot a \cdot c}}{2 \cdot a} &s=4$
Donde 4 es el tamaño equivalente al tamaño \LARGE en LaTeX. Obtenemos el siguiente resultado:

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Cambiando los colores
Por defecto, el color de los imágenes PNG que contienen los caracteres y símbolos especiales que genera WordPress es, color negro en primer plano y color blanco en segundo plano. En algunos casos, estos colores se adaptan a su entorno, pero no siempre es el caso, por lo tanto, es necesario definir el color.
Para esto se usa la instrucción &bg=[color de segundo plano] y la instrucción &fg=[color de primer plano] antes de cerrar el entorno, donde «[color de segundo plano]» y «[color de segundo plano]» son números RGB en formato hexadecimal (de seis cifras) que varía desde 000000 (equivalente al color negro) hasta FFFFFF (equivalente al color blanco). En la página web color-hex, puede consultar toda la variación de colores posible.
Si escribimos el siguiente texto, modificamos el color de segundo plano:
$latex \dfrac{-b \pm \sqrt{b^2-4 \cdot a \cdot c}}{2 \cdot a} &bg=eaca67$
Obteniendo el siguiente resultado:

Si escribimos el siguiente texto, modificamos el color de primer plano:
$latex \dfrac{-b \pm \sqrt{b^2-4 \cdot a \cdot c}}{2 \cdot a} &fg=389855$
Obteniendo el siguiente resultado:

Si escribimos el siguiente texto, modificamos el color de primer plano y de segundo plano al mismo tiempo:
$latex \dfrac{-b \pm \sqrt{b^2-4 \cdot a \cdot c}}{2 \cdot a} &bg=50384e&fg=a9d1d1$
Obteniendo el siguiente resultado:

Si escribimos el siguiente texto, modificamos el color de primer plano, de segundo plano y el tamaño al mismo tiempo:
$latex \dfrac{-b \pm \sqrt{b^2-4 \cdot a \cdot c}}{2 \cdot a} &bg=cfe8cd&fg=194775&s=3$
Obteniendo el siguiente resultado:

WordPress Latex Shortcode
La escritura en WordPress se basa en bloques con formatos prediseñados en los que podemos escribir nuestro contenido, entre ellos están los bloques custom html y shortcode; en ambos bloques es posible usar el shortcode (código corto) que permite escribir códigos de LaTeX más complejos de los que podemos escribir usando el entorno $latex $. También se puede ejecutar de dos formas:
- En la línea (inline math): se deben encerrar las instrucciones entre el siguiente entorno
[latex] [/latex]
- Desplegado (display math): se usa la instrucción \displaystyle una vez que se abre el entorno de la siguiente forma:
[latex] \displaystyle [/latex]
Hay que destacar que el código corto se debe usar sólo una vez en un bloque o usar un bloque dedicado para que no haya conflicto con entre los entornos. En mi experiencia, la mejor opción es la de usar un bloque custom html para escribir códigos horizontalmente muy grandes. De esta forma, si escribimos el siguiente texto:
<!-- wp:html -->
[latex] \huge
{\begin{array}{c|cccc}
& 4 & 1 & -3 & 5 \\
1 & \downarrow & 4 & 5 & 2 \\ \hline
& 4 & 5 & 2 & \multicolumn{1}{|c}{7} \\ \cline{5-5}
\end{array}}
[/latex]
<!-- /wp:html -->
Obtenemos el siguiente resultado:

Es importante destacar que para escribir arreglos, por alguna razón el carácter & pareciera estar reservado, así que sustituyéndolo por & pareciera solventar la situación.
Nota: El tamaño y los colores se modificarán de la misma forma que se hacen al escribir un documento LaTeX, así que no hay que recurrir a las instrucciones especiales de WordPress para hacer este tipo de alteraciones.



Debe estar conectado para enviar un comentario.