Autor: Anthonny Arias-García

Sub-Coordinador de Matemáticas de la Facultad de Ciencias Económicas y Sociales, Universidad de Los Andes, Mérida, Venezuela.

R: Los intervalos de confianza

Anthonny Arias-García1 comentario

Una vez que hemos calculado los estimadores de la Función de Regresión Muestral, es decir, \hat{\beta}_1 y \hat{\beta}_i sabiendo que estos cálculos están basados en una muestra, debemos ser cautelosos con las afirmaciones que derivan a partir de dichos estimadores, es por esto que debemos determinar una forma de medir qué tan confiables son estos cálculos.

También pudiera interesarte

¿Qué es un intervalo de confianza?

Habiendo definido el error estándar como una herramienta para medir qué tan precisos son nuestros estimadores, resulta intuitivo, definir un entorno en el que viven nuestros estimadores basado en el error estándar. Generalmente, esto se hace considerando intervalos centrados en el estimador de longitud igual a dos, cuatro y hasta seis veces el error estándar, esperando que este intervalo contenga el verdadero parámetro (de la Función de Regresión Poblacional) con un cierto grado de confianza.

Recordando que al contar únicamente con muestras, los verdaderos parámetros de la Función de Regresión Poblacional son desconocidos, consideremos particularmente, que queremos determinar qué tan cerca está el estimador \hat{\beta}_i del verdadero parámetro $\beta_i$, para esto se consideran dos números positivos \delta y \alpha (0 \leq \alpha \leq 1) de modo que la probabilidad de que el intervalo aleatorio (\hat{\beta}_i - \delta, \hat{\beta}_i + \delta) contenga al verdadero \beta_i sea igual a 1 - \alpha, es decir,

P(\hat{\beta}_i - \delta \leq \beta_i \leq \hat{\beta}_i + \delta) = 1 - \alpha

A partir de esta igualdad podemos identificar algunos elementos:

(\hat{\beta}_i - \delta, \hat{\beta}_i + \delta) es el intervalo de confianza y este intervalo pudiera no contener al verdadero valor.

Los extremos del intervalo de confianza se conocen como límites de confianza, donde (\hat{\beta}_i - \delta) es el límite de confianza inferior y (\hat{\beta}_i + \delta) es el límite de confianza superior.

1-\alpha es el coeficiente de confianza, en la práctica, 1 - \alpha suele expresarse en forma porcentual como 100(1 -\alpha)\%.

\alpha es el nivel de significancia, en la práctica, \alpha suele expresarse en forma porcentual como 100 \alpha.

El nivel de significancia también es conocido como la probabilidad de cometer un error tipo I. Recordando que

  • un error tipo I consiste en rechazar una hipótesis verdadera
  • un error tipo II consiste en no rechazar una hipótesis falsa.
En el primer panel se lee: Usted está embarazado.
En el segundo panel se lee: Usted no está embaraza.

Intervalos de confianza de los estimadores

Considerando el supuesto de que los residuos u_i siguen una distribución normal, podemos concluir que los estimadores de Mínimos Cuadrados Ordinarios \hat{\beta}_1 y \hat{\beta}_i son en sí mismos normalmente distribuidos con sus medias y varianzas correspondientes. Sabiendo esto, podemos definir una variable Z distribuida normalmente con media cero y varianza igual a uno, de la siguiente forma:

Z = \dfrac{\hat{\beta}_i - \beta_i}{ee(\hat{\beta}_i)} = \dfrac{(\hat{\beta}_i - \beta_i) \sqrt{\sum x_i^2}}{\sigma}

Así, se puede utilizar la distribución normal para hacer afirmaciones probabilísticas sobre \beta_i, siempre que se conozca la verdadera varianza poblacional \sigma^2.

Si se conoce \sigma^2, una propiedad importante de una variable normalmente distribuida con media \mu y varianza \sigma^2 es que el área bajo la curva normal entre \mu \pm \sigma es cercana a 68%, que entre \mu \pm 2\sigma es alrededor de 95%, y que entre los límites \mu \pm 3\sigma el área es cercana a 99.7%.

Distribución normal dos sigma | totumat.com
Distribución normal cuatro sigma | totumat.com
Distribución normal seis sigma | totumat.com

Pero pocas veces se conoce el verdadero valor de \sigma^2 y, en la práctica, está determinada por el estimador insesgado \sigma^2. Entonces, si en nuestra variable estandarizada Z, se reemplaza \sigma por \hat{\sigma}, tenemos que

t = \dfrac{\hat{\beta}_i - \beta_i}{ee(\hat{\beta}_i)} = \dfrac{(\hat{\beta}_i - \beta_i) \sqrt{\sum x_i^2}}{\hat{\sigma}}

Es posible demostrar que la variable t, así definida, sigue la distribución t con n-2 grados de libertad. Por consiguiente, en lugar de utilizar la distribución normal, se puede utilizar la distribución t para construir un intervalo de confianza para \beta_i de la siguiente forma:

P(-t_{\alpha/2} \leq t \leq t_{\alpha/2} ) = 1-\alpha

donde t_{\alpha/2} es el valor de la variable t obtenida de la distribución t para un nivel de significancia de \alpha/2 y n-2 grados de libertad; a menudo se denomina el valor crítico t a un nivel de significancia \alpha/2.

Considerando t=\dfrac{(\hat{\beta}_i - \beta_i) \sqrt{\sum x_i^2}}{\hat{\sigma}}, podemos considerar el siguiente intervalo de confianza.

P \left[ -t_{\alpha/2} \leq \dfrac{\hat{\beta}_i - \beta_i}{ee(\hat{\beta}_i)} \leq t_{\alpha/2} \right] = 1-\alpha

Intervalo de confianza para \hat{\beta}_2

Considerando la ecuación

P \left[ -t_{\alpha/2} \leq \dfrac{\hat{\beta}_2 - \beta_2}{ee(\hat{\beta}_2)} \leq t_{\alpha/2} \right] = 1-\alpha

Podemos manipular algebraicamente, para obtener que

P \left[ \hat{\beta}_2 - t_{\alpha/2} ee(\hat{\beta}_2) \leq \beta_2 \leq \hat{\beta}_2 + t_{\alpha/2} ee(\hat{\beta}_2) \right] = 1-\alpha

Esta ecuación proporciona un intervalo de confianza para \beta_2 de 100 (1 - \alpha)\%, que se escribe en forma más compacta como

\hat{\beta}_2 \pm t_{\alpha/2} ee(\hat{\beta}_2)

Calculamos los límites de confianza en R usando la siguiente sintaxis:

li.beta2 <- beta2 - qt(1-alpha/2, df=length(X)-2)*ee.beta2
ls.beta2 <- beta2 - qt(1-alpha/2, df=length(X)-2)*ee.beta2

Intervalo de confianza para 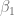\beta_1

Considerando la ecuación

P \left[ -t_{\alpha/2} \leq \dfrac{\hat{\beta}_1 - \beta_1}{ee(\hat{\beta}_1)} \leq t_{\alpha/2} \right] = 1-\alpha

Podemos manipular algebraicamente, para obtener que

P \left[ \hat{\beta}_1 - t_{\alpha/2} ee(\hat{\beta}_1) \leq \beta_1 \leq \hat{\beta}_1 + t_{\alpha/2} ee(\hat{\beta}_1) \right] = 1-\alpha

Esta ecuación proporciona un intervalo de confianza para \beta_1 de 100 (1 - \alpha)\%, que se escribe en forma más compacta como

\hat{\beta}_1 \pm t_{\alpha/2} ee(\hat{\beta}_1)

Calculamos los límites de confianza en R usando la siguiente sintaxis:

li.beta1 <- beta1 - qt(1-alpha/2, df=length(X)-2)*ee.beta1
ls.beta1 <- beta1 - qt(1-alpha/2, df=length(X)-2)*ee.beta1

Intervalo de confianza para \sigma^2

Considerando el supuesto de que los residuos u_i siguen una distribución normal, podemos concluir que la variable

\chi^2 = (n-2) \dfrac{\hat{\sigma}^2}{\sigma^2}

sigue la distribución \chi^2 con n-1 grados de libertad. Por lo tanto, con la distribución \chi^2 se establece el intervalo de confianza para \sigma^2

P(\chi^2_{1-\alpha/2} \leq \chi^2 \leq \chi^2_{\alpha/2}) = 1-\alpha

Donde \chi^2_{1-\alpha/2} y \chi^2_{\alpha/2} son dos valores de \chi^2 (los valores críticos \chi^2 ) obtenidos de la tabla chi cuadrado para n-2 grados de libertad de manera que ellos cortan 100{\alpha/2}\% de las áreas de las colas de la distribución \chi^2.

Distribución Chi-Cuadrado con nivel de significancia | totumat.com

Sustituyendo \chi^2 por (n-2) \dfrac{\hat{\sigma}^2}{\sigma^2} y operando algebraicamente en la inecuación, tenemos que

P \left[ (n-2) \dfrac{\hat{\sigma}^2}{\chi^2_{\alpha/2}} \leq \sigma^2 \leq (n-2) \dfrac{\hat{\sigma}^2}{\chi^2_{1-\alpha/2}} \right] = 1-\alpha

que da el intervalo de confianza a 100(1 - \alpha)\% para \sigma^2.

li.var <- (n-2)*sigma2.e/qchisq(alpha/2,df=length(X)-2)
ls.var <- (n-2)*sigma2.e/qchisq(1-alpha/2,df=length(X)-2)

Ejemplo

Consideremos un pequeño conjunto de datos, particularmente, los datos que se encuentran en la Tabla 3.2 del libro de Econometría de Damodar N. Gujarati and Dawn Porter en su quinta edición. Este conjunto de datos proporciona los datos primarios que se necesitan para estimar el efecto cuantitativo de la escolaridad en los salarios:

ObservaciónSalarioEscolaridad
14.45676
25.777
35.97878
47.33179
57.318210
66.584411
77.818212
87.835113
911.022314
1010.673815
1110.836116
1213.61517
1313.53118
Tabla 3.2

Una vez que hemos calculado el modelo lineal que define este conjunto de datos y en consecuencia, los parámetros estimados. Con un nivel de significancia de 5%, es decir, \alpha=0.05, podemos calcular los intervalos de confianza de ambos estimadores y además, el intervalo de confianza de la desviación estándar estimada, para esto, usamos la siguiente sintaxis:

# Nivel de Significancia
alpha <- 0.05

# Intervalo de Confianza de beta2
li.beta2 <- beta2 - qt(alpha/2, df=length(escolaridad)-2,lower.tail=F)*ee.beta2
ls.beta2 <- beta2 + qt(alpha/2, df=length(escolaridad)-2,lower.tail=F)*ee.beta2

# Intervalo de Confianza de beta1
li.beta1 <- beta1 - qt(alpha/2, df=length(escolaridad)-2,lower.tail=F)*ee.beta1
ls.beta1 <- beta1 + qt(alpha/2, df=length(escolaridad)-2,lower.tail=F)*ee.beta1

# Intervalo de Confianza de sigma2
li.sigma2 <- (length(escolaridad)-2)*sigma2.e/qchisq(alpha/2,df=length(escolaridad)-2,lower.tail=F)
ls.sigma2 <- (length(escolaridad)-2)*sigma2.e/qchisq(1-alpha/2,df=length(escolaridad)-2,lower.tail=F)

Al ejecutar estas instrucciones obtenemos que el intervalo de confianza del parámetro \hat{\beta}_2 es igual a

( 0.5709492 \ ; \ 0.8772442 )

y por lo tanto, concluimos que la probabilidad de que el intervalo (aleatorio) que allí aparece incluya al verdadero \beta_2 es de 0.95,

Al ejecutar estas instrucciones obtenemos que el intervalo de confianza del parámetro \hat{\beta}_1 es igual a

( -1.939487 \ ; \ 1.910582 )

y por lo tanto, concluimos que la probabilidad de que el intervalo (aleatorio) que allí aparece incluya al verdadero \beta_1 es de 0.95.

Al ejecutar estas instrucciones obtenemos que el intervalo de confianza del parámetro \sigma^2 es igual a

( 0.4421892 \ ; \ 2.540212 )

y por lo tanto, concluimos que la probabilidad de que el intervalo (aleatorio) que allí aparece incluya al verdadero \sigma^2 es de 0.95.

En su pantalla debería aparecer:

Ejercicios Propuestos

Ejercicios Propuestos – Operaciones entre Conjuntos

Anthonny Arias-García2 comentarios

Tomando en cuenta las operaciones básicas entre conjuntos, escriba de forma extensiva los conjuntos resultantes al efectuar las operaciones indicadas.

Anuncios
  1. Considerando un conjunto universal:

U = {a, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, x, y, z}

y los siguientes conjuntos pertenecientes a este conjunto universal:

A = {x, b, s, k, c, o, f, q, t, h, e, ñ, w, p, j, g, d, u, a, n, y, r}

B = {y, ñ, m, e, z, a, k, u, q, s, c, l, d, x}

Calcule A \cup B, A \cap B, A' y B'.

  1. Considerando un conjunto universal:

U = {a, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, x, y, z}

y los siguientes conjuntos pertenecientes a este conjunto universal:

A = {f, i, j, v, a, y}

B = {z, g, p, e, o, w, h, j, n, f, r, a, s, v, l, u}

Calcule A \cup B, A \cap B, A' y B'.

  1. Considerando un conjunto universal:

U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}

y los siguientes conjuntos pertenecientes a este conjunto universal:

A = {13, 9, 2, 1, 12, 3, 6, 5, 14}

B = {4, 11, 1, 14, 10, 9, 2, 13, 15, 5, 8, 7, 12}

Calcule A \cup B, A \cap B, A' y B'.

  1. Considerando un conjunto universal:

U = {recta, punto, ángulo, triángulo, cuadrilátero, rectángulo, rombo, trapecio, pentágono, hexágono, heptágono, octágono}

y los siguientes conjuntos pertenecientes a este conjunto universal:

A = {punto, octágono}

B = {rombo, trapecio, ángulo, cuadrilátero, pentágono, octágono, punto}

Calcule A \cup B, A \cap B, A' y B'.

  1. Considerando un conjunto universal:

U = {a, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, x, y, z}

y los siguientes conjuntos pertenecientes a este conjunto universal:

A = {v, w, q, k, g, b, j, n, i, p, l, m, a, ñ, x, f, u, y, r, o, h, e, d, c, z, t, s}

B = {y, ñ, r, d, j, m, k, s}

Calcule A \cup B, A \cap B, A' y B'.

  1. Considerando un conjunto universal:

U = {recta, punto, ángulo, triángulo, cuadrilátero, rectángulo, rombo, trapecio, pentágono, hexágono, heptágono, octágono}

y los siguientes conjuntos pertenecientes a este conjunto universal:

A = {cuadrilátero, hexágono, rombo}

B = {heptágono, ángulo}

Calcule A \cup B, A \cap B, A' y B'.

  1. Considerando un conjunto universal:

U = {recta, punto, ángulo, triángulo, cuadrilátero, rectángulo, rombo, trapecio, pentágono, hexágono, heptágono, octágono}

y los siguientes conjuntos pertenecientes a este conjunto universal:

A = {rombo, recta, heptágono, hexágono, punto, ángulo, pentágono}

B = {heptágono, rectángulo, cuadrilátero, rombo, recta, punto, ángulo, octágono, hexágono, triángulo, pentágono, trapecio}

Calcule A \cup B, A \cap B, A' y B'.

  1. Considerando un conjunto universal:

U = {ecuaciones, inecuaciones, polinomios, rectas, funciones, límites, derivas, integrales, matrices, sucesiones, geometría, aritmética}

y los siguientes conjuntos pertenecientes a este conjunto universal:

A = {inecuaciones, aritmética, geometría}

B = {ecuaciones, integrales, inecuaciones, rectas, sucesiones, matrices}

Calcule A \cup B, A \cap B, A' y B'.

También pudiera interesarte

  1. Considerando un conjunto universal:

U = {ecuaciones, inecuaciones, polinomios, rectas, funciones, límites, derivas, integrales, matrices, sucesiones, geometría, aritmética}

y los siguientes conjuntos pertenecientes a este conjunto universal:

A = {ecuaciones, límites, geometría, polinomios, aritmética}

B = {polinomios, integrales, matrices, derivas, funciones, geometría, rectas}

Calcule A \cup B, A \cap B, A' y B'.

  1. Considerando un conjunto universal:

U = {ecuaciones, inecuaciones, polinomios, rectas, funciones, límites, derivas, integrales, matrices, sucesiones, geometría, aritmética}

y los siguientes conjuntos pertenecientes a este conjunto universal:

A = {integrales, funciones, derivas, rectas, ecuaciones, polinomios, aritmética, matrices, inecuaciones}

B = {rectas, geometría, integrales, derivas}

Calcule A \cup B, A \cap B, A' y B'.

  1. Considerando un conjunto universal:

U = {a, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, x, y, z}

y los siguientes conjuntos pertenecientes a este conjunto universal:

A = {o, ñ, p, w, a, z, e, b, x, u, n, i, q, l, t, r, v, m, g, y}

B = {i, k}

Calcule A \cup B, A \cap B, A' y B'.

  1. Considerando un conjunto universal:

U = {recta, punto, ángulo, triángulo, cuadrilátero, rectángulo, rombo, trapecio, pentágono, hexágono, heptágono, octágono}

y los siguientes conjuntos pertenecientes a este conjunto universal:

A = {cuadrilátero, trapecio, rectángulo, heptágono, punto, ángulo, rombo}

B = {ángulo, triángulo, rectángulo}

Calcule A \cup B, A \cap B, A' y B'.

  1. Considerando un conjunto universal:

U = {a, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, x, y, z}

y los siguientes conjuntos pertenecientes a este conjunto universal:

A = {j, z, p, k, i, t, u, s, x, m, l, v, w, r, e, o, a, h}

B = {y, x, l, a, r, c, m, q, i, t, w, b, d, e, s}

Calcule A \cup B, A \cap B, A' y B'.

  1. Considerando un conjunto universal:

U = {a, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, x, y, z}

y los siguientes conjuntos pertenecientes a este conjunto universal:

A = {b, g, w, i, u, d, ñ, v, a, o, y, z, r, t}

B = {s}

Calcule A \cup B, A \cap B, A' y B'.

  1. Considerando un conjunto universal:

U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}

y los siguientes conjuntos pertenecientes a este conjunto universal:

A = {3, 2, 9, 4, 12, 15, 1, 5, 7, 0, 8}

B = {5, 6, 7}

Calcule A \cup B, A \cap B, A' y B'.

  1. Considerando un conjunto universal:

U = {negro, azul, marrón, gris, verde, naranja, rosa, púrpura, rojo, blanco, amarillo}

y los siguientes conjuntos pertenecientes a este conjunto universal:

A = {rosa}

B = {blanco, amarillo, gris, rosa, rojo, azul}

Calcule A \cup B, A \cap B, A' y B'.

Tomando en cuenta las operaciones básicas entre conjuntos, escriba de forma extensiva los conjuntos resultantes al efectuar las operaciones indicadas.

Anuncios

R: El coeficiente de correlación r

Anthonny Arias-García1 comentario

Hemos visto que el coeficiente de determinación nos permite determinar en qué medida dos variables están relacionadas, pero siempre resulta de interés preguntarse si es posible determinar la forma en que estas dos variables están relacionadas, particularmente, en qué medida están correlacionadas.

También pudiera interesarte

Coeficiente de Correlación Muestral

Considerando una de las fórmulas para calcular el coeficiente de determinación r^2, definimos un nuevo valor que está íntimamente relacionado con dicha fórmula pero que conceptualmente son diferentes. Entonces, partiendo del hecho que,

r^2 = \dfrac{(\sum x_i y_i)^2}{\sum x_i^2 \sum y_i^2}

Definimos un nuevo valor r, conocido como el Coeficiente de Correlación Muestral, que mide el grado de asociación lineal entre dos variables y se calcula de la siguiente forma:

r = \dfrac{\sum x_i y_i}{\sqrt{\sum x_i^2 \sum y_i^2}}

Podemos calcularlo en R usando la siguiente sintaxis:

r <- sum((X-m.X)*(Y-m.Y))/sqrt(sum((X - m.X)^2)*sum((Y - m.Y)^2))

Es importante destacar que:

Aunque el coeficiente de correlación r es una medida de asociación lineal entre dos variables, este no implica necesariamente alguna relación causa-efecto.

Una ventaja en el cálculo de este coeficiente, es que es simétrico por la forma en que está definido, es decir, el coeficiente de correlación entre X y Y (r_{XY}) es el mismo que entre Y y X (r_{YX}).

Interpretación Gráfica del Coeficiente de Correlación Muestral

A diferencia de r^2, que está acotado por 0 y 1; el coeficiente de correlación muestral está acotado por -1 y 1, esto quiere decir que puede tomar valores negativos. Entonces, considerando que gráficamente es independiente del origen y de la escala, podemos considerar varias observaciones sobre este valor:

Si valor del coeficiente de correlación r es exactamente igual a 1 (uno positivo), los datos están representados gráficamente sobre una línea recta creciente.

Interpretación Gráfica del Coeficiente de Correlación Muestral, r=1 | totumat.com

Si valor del coeficiente de correlación r es exactamente igual a -1 (uno negativo), los datos están representados gráficamente sobre una línea recta decreciente.

Interpretación Gráfica del Coeficiente de Correlación Muestral, r=-1 | totumat.com

Si valor del coeficiente de correlación r está cercano a 1 (uno positivo), los datos representados gráficamente, tienen una clara tendencia lineal creciente pero no están exactamente alineados.

Interpretación Gráfica del Coeficiente de Correlación Muestral, r cerca de 1 | totumat.com

Si valor del coeficiente de correlación r está cercano a -1 (uno negativo), los datos representados gráficamente, tienen una clara tendencia lineal decreciente pero no están exactamente alineados.

Interpretación Gráfica del Coeficiente de Correlación Muestral, r cerca de -1 | totumat.com

Si valor del coeficiente de correlación r está cercano a 0 pero es positivo, los datos representados gráficamente, tienen una tendencia lineal creciente pero presentan una dispersión mayor a media que el valor de r está más cercano a cero.

Interpretación Gráfica del Coeficiente de Correlación Muestral, r cerca de 0 pero positivo | totumat.com

Si valor del coeficiente de correlación r está cercano a 0 pero es negativo, los datos representados gráficamente, tienen una tendencia lineal decreciente pero presentan una dispersión mayor a media que el valor de r está más cercano a cero.

Interpretación Gráfica del Coeficiente de Correlación Muestral, r cerca de 0 pero negativo | totumat.com

Si la variable Y y la variable X son estadísticamente independientes, entonces valor del coeficiente de correlación r es igual a cero y en este caso, los datos representados gráficamente, no presentan ningún tipo de tendencia lineal.

Interpretación Gráfica del Coeficiente de Correlación Muestral, r igual a cero | totumat.com

Precaución: El coeficiente de correlación r es una medida de asociación lineal (o dependencia lineal) solamente; su uso en la descripción de relaciones no lineales no tiene significado. Dicho esto, puede ocurrir que r sea igual a cero pero el conjunto de datos presente otro tipo de relación.

Interpretación Gráfica del Coeficiente de Correlación Muestral, r igual a cero pero Y=X^2 | totumat.com

Ejemplo

Consideremos un pequeño conjunto de datos, particularmente, los datos que se encuentran en la Tabla 3.2 del libro de Econometría de Damodar N. Gujarati and Dawn Porter en su quinta edición. Este conjunto de datos proporciona los datos primarios que se necesitan para estimar el efecto cuantitativo de la escolaridad en los salarios:

ObservaciónSalarioEscolaridad
14.45676
25.777
35.97878
47.33179
57.318210
66.584411
77.818212
87.835113
911.022314
1010.673815
1110.836116
1213.61517
1313.53118
Tabla 3.2

Una vez que hemos calculado el modelo lineal que define este conjunto de datos, podemos calcular el coeficiente de determinación para ver qué tan relacionadas están las variables Salario y Escolaridad, para esto, usamos la siguiente sintaxis:

r <- sum((escolaridad-m.escolaridad)*(salario-m.salario))/sqrt(sum((escolaridad - m.escolaridad)^2)*sum((salario - m.salario)^2))

Al ejecutar estas instrucciones obtenemos coeficiente de correlación r, que en este caso es igual a 0.9527809.

En su pantalla debería aparecer:

En este caso, el valor del coeficiente de correlación sugiere que la variable Y y la variable X definen un tendencia lineal creciente y es lo que se puede observar en el gráfico de dispersión.

Gráfico de Dispersión

R: El coeficiente de determinación r²

Anthonny Arias-GarcíaDeja un comentario

Una vez que hemos calculado la función de regresión muestral como un modelo lineal a partir de un conjunto de datos, podemos notar en su gráfica que las observaciones no necesariamente caen sobre la línea que describe dicha función y aunque esta sería situación ideal (pues así podemos describir con precisión todo el conjunto de datos usando una función), esto no ocurre en la realidad.

También pudiera interesarte

La bondad de ajuste

Considerando el siguiente gráfico, si todas las observaciones cayeran en la línea de regresión, obtendríamos lo que se conoce como un ajuste perfecto, pero rara vez se presenta este caso. Por lo general los valores de \hat{u}_i pueden ser positivos o negativos, gráficamente, podemos decir que algunas observaciones estarán por encima de la línea de regresión y otras por debajo.

Diagrama de Dispersión y Línea de Regresión | totumat.com

Aunque se tiene la esperanza de que los residuos alrededor de la línea de regresión sean lo más pequeños posibles, el coeficiente de determinación r^2 (caso de dos variables) o R^2 (regresión múltiple) es una medida comprendida que dice que tan bien se ajusta la línea de regresión muestral a los datos.

Antes de mostrar cómo calcular r^2, consideremos Diagramas de Venn para entender qué representa el valor de r^2, de forma que: el círculo Y, representa la variación en la variable dependiente Y; el círculo X, la variación en la variable explicativa X.

Si estos dos círculos no se intersectan, entonces la variación en Y no es explicada por la variación en X. El valor de r^2 que representa esta situación, es r^2=0

El coeficiente de determinación r² | totumat.com

La intersección de los dos círculos (el área sombreada) indica la medida en la cual la variación en Y se explica por la variación en X.

Entre mayor sea el área de la intersección, mayor será la variación en Y que se explica por la variación de X. r^2 es tan sólo una medida numérica de esta intersección y generalmente es un valor entre 0 y 1.

El coeficiente de determinación r² | totumat.com

Si estos dos círculos se intersectan en su totalidad, es decir, son iguales, entonces la variación en Y está explicada en su totalidad por la variación de la variable X. El valor de r^2 que representa esta situación, es r^2=1

El coeficiente de determinación r² | totumat.com

Para calcular r^2, partimos del hecho que Y_i = \hat{Y}_i + \hat{u}_i, que expresado en forma de desviación, es decir, como la diferencia de cada observación con la media,

y_i = \hat{y}_i + \hat{u}_i

Al elevar al cuadrado esta última ecuación en ambos lados y sumar sobre la muestra, obtenemos

\sum y_i^2

= \sum \hat{y}_i^2 + \sum \hat{u}_i^2 + 2\sum \hat{y}_i \hat{u}_i

= \sum \hat{y}_i^2 + \sum \hat{u}_i^2

= \hat{\beta}_2^2 \sum \hat{x}_i^2 + \sum \hat{u}_i^2

Esa última igualdad se debe a que \sum \hat{y}_i \hat{u}_i = 0 y \hat{y}_i = \hat{\beta}_2 \hat{x}_i.

Las diversas sumas de cuadrados en esta ecuación se describen de la siguiente manera:

  • \sum y_i = \sum (Y_i - \overline{Y})^2 es la variación total de los valores reales de Y respecto de su media muestral, que puede denominarse la suma de cuadrados total (SCT).
  • \sum \hat{y}_i = \sum (\hat{y}_i - \overline{Y})^2 = \hat{\beta}_2^2 \sum \hat{x}_i^2 es la variación de los valores de Y estimados alrededor de su media, que apropiadamente puede llamarse la suma de cuadrados debida a la regresión (es decir, debida a la variable explicativa), o explicada por ésta, o simplemente la suma de cuadrados explicada (SCE).
  • \sum \hat{u}_i es la la variación residual o no explicada de los valores de Y alrededor de la línea de regresión, o sólo la suma de cuadrados de los residuos (SCR).

Por lo tanto, podemos reescribir la última ecuación de la siguiente manera:

SCT = SCE + SCR

Demostrando así, que la variación total en los valores Y observados alrededor del valor de su media puede dividirse en dos partes, una atribuible a la línea de regresión y la otra a fuerzas aleatorias, pues no todas las observaciones Y caen sobre la línea ajustada.

Dividiendo esta ecuación, entre la SCT a ambos lados tenemos que

1 = \dfrac{SCE}{SCT} + \dfrac{SCR}{SCT}

= \dfrac{\sum (\hat{y}_i - \overline{Y})^2}{\sum (Y_i - \overline{Y})^2} + \dfrac{ \sum \hat{u}_i^2}{\sum (Y_i - \overline{Y})^2}

Finalmente, definimos el coeficiente de determinación r^2 como

r^2 = \dfrac{SCE}{SCT} = \dfrac{\sum (\hat{y}_i - \overline{Y})^2}{\sum (Y_i - \overline{Y})^2}

Podemos calcularlo en R usando la siguiente sintaxis:

r2 <- sum((Y.e - m.Y)^2)/sum((Y - m.Y)^2)

También podemos definir el coeficiente de determinación r^2 como

r^2 = 1 - \dfrac{SCR}{SCT} = 1 - \dfrac{ \sum \hat{u}_i^2}{\sum (Y_i - \overline{Y})^2}

Podemos calcularlo en R usando la siguiente sintaxis:

r2 <- 1 - sum((Y - Y.e)^2)/sum((Y - m.Y)^2)

Ejemplo

Consideremos un pequeño conjunto de datos, particularmente, los datos que se encuentran en la Tabla 3.2 del libro de Econometría de Damodar N. Gujarati and Dawn Porter en su quinta edición. Este conjunto de datos proporciona los datos primarios que se necesitan para estimar el efecto cuantitativo de la escolaridad en los salarios:

ObservaciónSalarioEscolaridad
14.45676
25.777
35.97878
47.33179
57.318210
66.584411
77.818212
87.835113
911.022314
1010.673815
1110.836116
1213.61517
1313.53118
Tabla 3.2

Una vez que hemos calculado el modelo lineal que define este conjunto de datos, podemos calcular el coeficiente de determinación para ver qué tan relacionadas están las variables Salario y Escolaridad, para esto, usamos la siguiente sintaxis:

r2 <- sum((salario.e - m.salario)^2)/sum((salario - m.salario)^2)

Al ejecutar estas instrucciones obtenemos coeficiente de determinación r^2, que en este caso es igual a 0.9077914.

En su pantalla debería aparecer:

Resultados de R, Coeficiente de Determinación r cuadrado. | totumat.com

En este caso, el valor del coeficiente de determinación sugiere que la variación en Y está explicada casi en su totalidad por la variación de la variable X.

Varianza y Error estándar

R: El error estándar

Anthonny Arias-García2 comentarios

El Método de los Mínimos Cuadrados Ordinarios (MCO) nos provee una forma estimar los parámetros \hat{\beta}_2 y \hat{\beta}_1, sin embargo, al estar estos valores condicionados a la muestra que se tome, es probable que entre una muestra y otra, estos valores presenten variaciones. Entonces, surge la pregunta: ¿de qué forma podemos garantizar precisión en las estimaciones? O al menos, ¿podemos medir la imprecisión de estas?

También pudiera interesarte

La varianza muestral y el error estándar

La teoría estadística provee una forma de medir la precisión de un valor estimado, esto es, el error estándar (ee) que está definido como la desviación estándar de la distribución muestral del estimador. Es importante recalcar que al hablar sólo de desviación estándar, hacemos referencia a la población, en cambio, al hablar del error estándar, hacemos referencia a la muestra de dicha población.

Considerando la varianza muestral, que mide la variabilidad de los datos respecto a su media; podemos calcular el error estándar al tomar la raíz cuadrada de esta. Entonces, si \sigma es la desviación estándar:

Calculamos la varianza y el error estándar del parámetro \hat{\beta}_2 usando las siguientes fórmulas respectivamente,

var(\hat{\beta}_2) = \dfrac{\sigma^2}{\sum x_i^2}

ee(\hat{\beta}_2) = \dfrac{\sigma}{ \sqrt{\sum x_i^2} }

Podemos calcular la varianza y el error estándar del parámetro \hat{\beta}_2 en R usando la siguiente sintaxis:

var.beta2 <- sigma2.e/sum( (Yd-m.Yd)^2 )
ee.beta2 <- sqrt(v.beta2)

Por otra parte calculamos la varianza y el error estándar del parámetro \hat{\beta}_1 usando las siguientes fórmulas respectivamente,

var(\hat{\beta}_1) = \dfrac{ \sum X_i^2 }{n \sum x_i^2} \cdot \sigma^2

ee(\hat{\beta}_1) = \sqrt{ \dfrac{ \sum X_i^2 }{n \sum x_i^2} } \cdot \sigma

Podemos calcular la varianza y el error estándar del parámetro \hat{\beta}_1 en R usando la siguiente sintaxis:

var.beta1 <- sigma2.e*sum( Yd^2 )/(length(Yd)*sum( (Yd-m.Yd)^2 ))
ee.beta1 <- sqrt(v.beta1)

La desviación estándar estimada y el error estándar de estimación

Si bien contamos con los datos para calcular parte de estas expresiones, aún desconocemos el valor de \sigma^2, pues este valor se obtiene a partir de la población pero sólo contamos con una muestra, afortunadamente, podemos definir una fórmula que nos estima a través de del Método de Mínimos Cuadrados Ordinarios a la verdadera pero desconocida \sigma^2, esta fórmula es

\hat{\sigma}^2 = \dfrac{\sum \hat{u}_i^2}{n-2}

Podemos calcular la desviación estándar estimada en R usando la siguiente sintaxis:

sigma2.e <- sum(res^2)/(lenght(X)-2)

Vale la pena destacar que la raíz cuadrada de \hat{\sigma}^2 se conoce como el error estándar de estimación o el error estándar de la regresión (eee). No es más que la desviación estándar de los valores Y alrededor de la línea de regresión estimada, la cual suele servir como medida para resumir la bondad del ajuste de dicha línea. Se calcula de la siguiente manera

\hat{\sigma} = \sqrt{\dfrac{\sum \hat{u}_i^2}{n-2}}

Podemos calcular este valor en R usando la siguiente sintaxis:

ee.e <- sqrt(sigma2.e)

Ejemplo

Consideremos un pequeño conjunto de datos, particularmente, los datos que se encuentran en la Tabla 3.2 del libro de Econometría de Damodar N. Gujarati and Dawn Porter en su quinta edición. Este conjunto de datos proporciona los datos primarios que se necesitan para estimar el efecto cuantitativo de la escolaridad en los salarios:

ObservaciónSalarioEscolaridad
14.45676
25.777
35.97878
47.33179
57.318210
66.584411
77.818212
87.835113
911.022314
1010.673815
1110.836116
1213.61517
1313.53118
Tabla 3.2

Una vez que hemos calculado el modelo lineal que define este conjunto de datos, podemos determinar el error estándar de los parámetros estimados, pero primero debemos estimar la desviación estándar usando la siguiente sintaxis:

sigma2.e <- sum( (residuos)^2 )/(length(salario)-2)

Podemos calcular la varianza y el error estándar del parámetro \hat{\beta}_2 en R usando la siguiente sintaxis:

var.beta2 <- sigma2.e/sum( (escolaridad-m.escolaridad)^2 )
ee.beta2 <- sqrt(var.beta2)

Al ejecutar estas instrucciones obtenemos error estándar del parámetro \hat{\beta}_2, que en este caso es igual a 0.06958134.

Podemos calcular la varianza y el error estándar del parámetro \hat{\beta}_1 en R usando la siguiente sintaxis:

var.beta1 <- sigma2.e*sum( escolaridad^2 )/(length(escolaridad)*sum( (escolaridad-m.escolaridad)^2 ))
ee.beta1 <- sqrt(var.beta1)

Al ejecutar estas instrucciones obtenemos error estándar del parámetro \hat{\beta}_1, que en este caso es igual a 0.8746239.

En su pantalla debería aparecer:

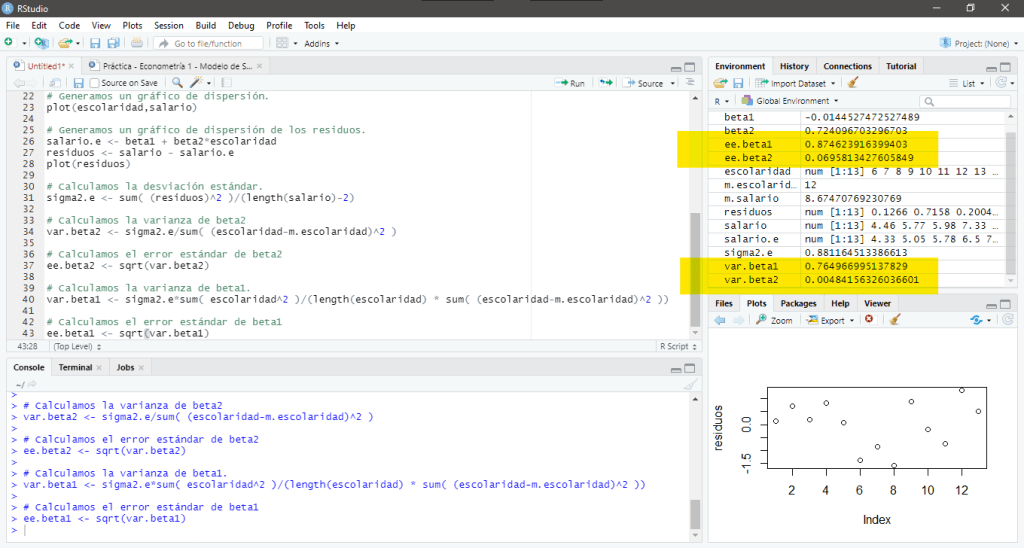
Varianza y Error Estándar de los parámetros en R. | totumat.com