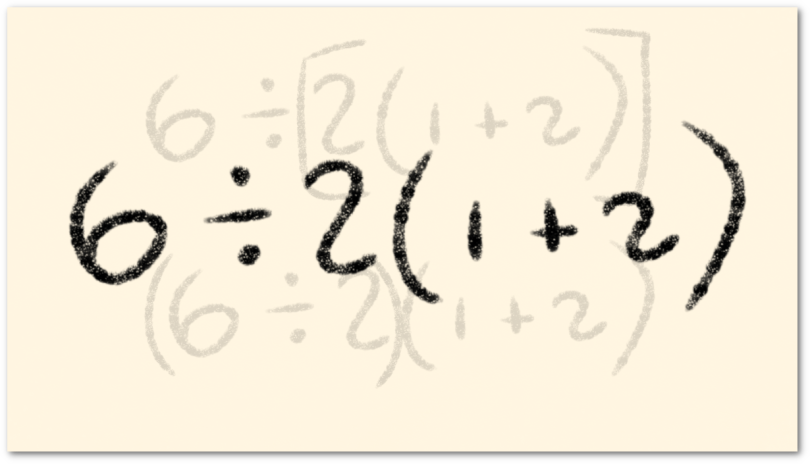In 2019 a debate went viral, discussing on what is the result of the operation 8÷2(2+2), I thought that it had been forgotten and that the situation had already been clarified. However, it was reborn on the infamous 2020 as 6÷2(1+2).
It is necessary to understand that when considering mixed operations, there is an established order among the operations. First all the products must be made, then all the divisions, then all the additions and finally all the subtractions. Also consider that if there are signs of grouping you must first solve the contents between parentheses ( ), then brackets [ ] and then braces { }; you must make the operations that are within them considering the original hierarchy between operations. This is what people call BODMAS.
Does calculators lie?
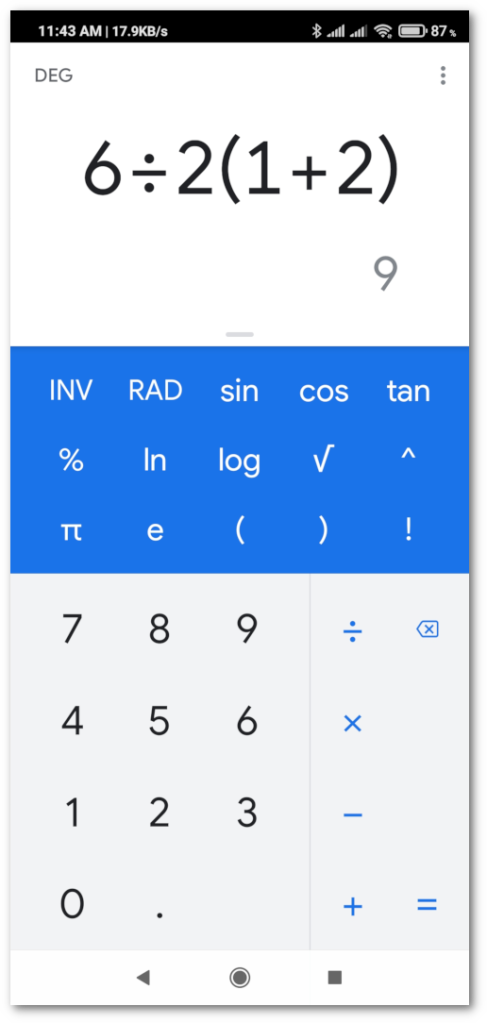

When calculating this operation in a calculator, the results will differ depending on how they have been programmed because some have been programmed to prioritize the order of operations and others have been programmed to prioritize the order of appearance of the operations.
Write it better…
In my opinion, the problem with that specific case is that the person who originally raised it does not have the slightest idea of how to use the grouping signs because when operations between numbers are proposed, they always come from a real problem, so that kind of problems will always be well proposed if they are written correctly. Ambiguity in mathematics should have no place.
This operation defined as it is, is like asking a question without question marks, commas, colons or semicolons.
How to propose the problem?
Case 1
Suppose that you work for a party agency and at a party you have been asked to distribute six pieces of cake to a pair of children, this situation is described with the operation 6÷2. Suppose furthermore that you have to do this twice more, then this situation is described with the following operation (6÷2)×2. If again you are told to do this one more times, then at the end you will describe this with the following operation
(6÷2)×(2+1)
= 3×3
= 9
This means that in the end you will have to distribute 9 pieces of cake.
Case 2
Suppose again that you work at a party agency and you have been given six pieces of cake to distribute to a pair children, this situation is described with operation 6÷2. However, you are being told that now it is not a pair of children but rather two pairs of children, this situation is described with the operation 6÷[2×2]. Finally, you are told that one more pair of children have arrived, so in the end you will describe this with the following operation
6÷[2×(2+1)]
= 6÷[2×3]
= 6÷6
= 1
This means that at the end you will have to give a piece of cake to each child.
In conclusion…
Considering these two cases, we notice that each one has its own approach and interpretation. Always specifying which operations have to be grouped together and always specifying which operations should be carried out first.