En la economía, la utilidad estudia el nivel de satisfacción de un individuo respecto a la forma en que este clasifica distintas situaciones, sin embargo, este tipo de funciones no se pueden cuantificar de forma rigurosa pues la satisfacción es algo muy subjetivo ya que la utilidad de una persona no sólo depende de los bienes materiales que consume, sino también de sus actitudes psicológicas, de las presiones de su grupo social, de sus experiencias personales y del entorno cultural en general según Walter Nicholson en su libro de Teoría Microeconómica, Principios básicos y ampliaciones, es por esto que se restringe el estudio de este tipo de funciones a variables que se puedan medir como las cantidades relativas de alimento, horas de trabajo semanales o tasas fiscales, las variables que no podemos medir se suponen como constantes, esto se le llama en los libros de texto económicos ceteris paribus.
También pudiera interesarte
Consideremos el caso particular en que una vez presentados bienes distintos, un individuo debe escoger cantidades
de dichos bienes. Entonces, representaremos la forma en que este individuo clasifica estos bienes definiendo una función de utilidad de la siguiente forma:
Cuando sólo se toman en consideración dos bienes, entonces la función de utilidad se expresa sólo para la cantidad de estos dos bienes y
:
La curva de nivel representa todas las combinaciones de
y
que proveen al individuo un nivel de satisfacción igual a
. Esta curva de nivel se llama curva de indiferencia pues al ellas representar todas las combinaciones de las canastas del mercado que proveen al individuo el mismo nivel de satisfacción, este se mostrará indiferente entre una canasta y otra. De forma general, si la función
es una función de Cobb-Douglas, su gráfica estará representada de la siguiente forma:

La curva de indiferencia además de mostrar las combinaciones de los bienes y
, nos permiten observar que en que medida un individuo está dispuesto a intercambiar los bienes para obtener el mismo nivel de satisfacción. De forma que si tiene las cantidades
y
de un bien, la cantidad de unidades de
que intercambia para obtener una unidad de
está definida como la tasa marginal de sustitución (TMS) y está determinada por la pendiente negativa de la curva
en el punto
, es decir,
Calculada a partir de la función implícita .
¿Cómo calcular la TMS?
Es posible determinar la tasa marginal de sustitución calculando derivadas parciales pues si tomamos en cuenta que el diferencial de la función de utilidad está dada por , entonces el diferencial de la curva de nivel
será
A partir de esta igualdad, podemos obtener la derivada haciendo un abuso de la notación para despejar los diferenciales de
y
de la siguiente forma
Ejemplos
Reduzcamos una situación en la que un individuo de la sociedad sólo puede dedicar su tiempo a dos usos respecto al mercado: horas de trabajo y horas de no trabajo.
Denotaremos las horas de trabajo con la variable (labor en inglés) y si por cada hora de trabajo obtiene un ingreso de
, entonces, considerando que este individuo puede adquirir bienes si trabaja, definimos la variable consumo
.
Definiremos las horas de no trabajo como horas de ocio y las denotaremos con la variable , estas representan las horas que dedica a trabajar en casa (no en el mercado), ver televisión o navegar en las redes sociales.
Suponga que las preferencias de este individuo están determinadas a través de la siguiente función de utilidad:
Para determinar la TMS. Debemos calcular ambas funciones de utilidad marginal. Previamente, debemos notar que , por lo tanto
Luego,

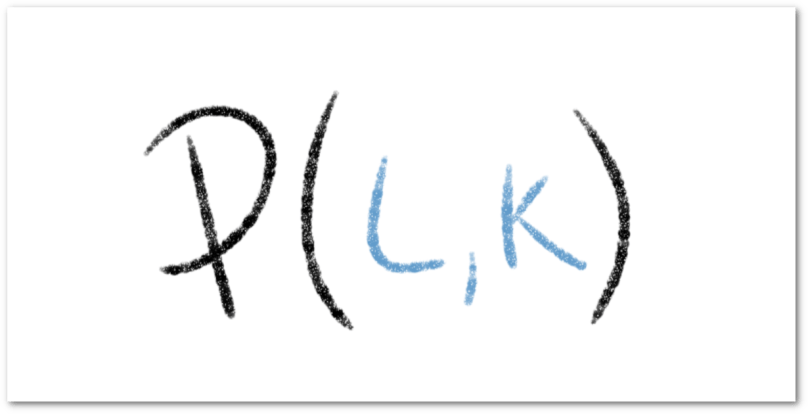
Debe estar conectado para enviar un comentario.